CS5: Introduction to Computer Science at Harvey Mudd College
CS5 Web > Homework8Gold > Lab8
Submissions: CS submission site

Lab 8: Creating the Mandelbrot Set

The Mandelbrot Set

In this lab you will build a program to visualize and explore the points in and near the Mandelbot Set. In doing so, you will have the chance to:


Introduction to for Loops!

Because you will create images in this lab, there is some additional starter code—grab and unzip hw8pr1.zip.

Here is hw8pr1.zip



Trying things out -- and making sure you have the Pillow library...

If you get an error that there is "no PIL" or "no object/library PIL," it's the Pillow library you need.
Try


Getting started on the lab...

Next, as a reminder of how loops work, first write two short functions in your hw8pr1.py file:

You'll use these ideas (through a variant of the update function) in building the Mandelbrot set, next:


Introduction to the Mandelbrot Set

The Mandelbrot set is a set of points in the complex plane that share an interesting property that is best explained through the following process:

The Mandelbrot set is the collection of all complex numbers c such that this process does not diverge to infinity as n gets large. In other words, for some c, if zn diverges to infinity (becomes unreasonably large) then c is not in the set; otherwise it is.


There are other, equivalent definitions of the Mandelbrot set. For example, the Mandelbrot set consists of those points in the complex plane for which the associated Julia set is connected. Of course, that requires defining Julia sets...which we won't do here.

The Mandelbrot set is a fractal, meaning that its boundary is so complex that it cannot be well approximated by one-dimensional line segments, regardless of how closely one zooms in on it. There are many available references on the topic.


The inMSet function

The next task is to write a function named inMSet(c, n) that accepts a complex number c and an integer n.

This function will return a Boolean:

First, we will introduce Python's built-in support for complex numbers.


Complex numbers in Python

In Python a complex number is represented in terms of its real part x and its imaginary part y:


Side notes:

Also, if you're not terribly familiar with complex numbers, no worries! You just need to know a few little things:


Try it out!    Just to get familiar with complex numbers, at the command-line Python prompt try 

In [1]: c = 3 + 4j

In [2]: c
Out[2]: (3+4j)

In [3]: abs(c)
Out[3]: 5.0

In [4]: c**2
Out[4]: (-7+24j)

Python is happy to use the power operator (**) and other operators with complex numbers. However, note that you cannot compare complex numbers directly with > or < — they are 2D points, so there's no "greater than"! Thus, you cannot write c > 2 for a complex c (it will "throw" a TypeError)

You CAN compare the magnitude of complex numbers, however: abs(c) > 2.

Note that the built-in abs function returns the magnitude of a complex number.


The inMSet function:

To determine whether or not a number c is in the Mandelbrot set, you will

to see if this sequence of z0, z1, z2, etc. stays bounded.

To put it another way, we need to know whether or not the magnitude of this zk sequence goes off toward infinity.


Truly determining whether or not this sequence goes off to infinity isn't feasible. To make a reasonable guess, we will have to decide on two things:

We will run the update process n times. The n is the second argument to the function inMSet(c, n). This is a value you will experiment with, but 25 is a good starting point.

The value for infinity can be surprisingly low! It has been shown that if the absolute value of a complex number z ever gets larger than 2 during the update process, then the sequence will definitely diverge to infinity!

There is no equivalent rule that tells us that the sequence definitely does not diverge, but it is very likely it will stay bounded if abs(z) does not exceed 2 after a reasonable number of iterations.

Our n is that "reasonable" number, starting at 25.


Writing the inMSet function

You should copy your update function and change its name to inMSet.

It's definitely better to copy and change that old function—do not call update directly.

To get you started, here is the first line and a docstring for inMSet: 

def inMSet(c, n):
    """inMSet accepts
            c for the update step of z = z**2+c
            n, the maximum number of times to run that step.
       Then, it returns
            False as soon as abs(z) gets larger than 2.
            True if abs(z) never gets larger than 2 (for n iterations).
    """

The inMSet function should return False if the sequence zn+1 = zn2 + c ever yields a z value whose magnitude is greater than 2. It returns True otherwise.

Note that you will not need different variables for z0, z1, z2, and so on. Rather, you'll use a single variable z. You'll update the value of z within a loop, just as in update.

Also, note that the loop should return False as soon as the value of z exceeds 2. If you try to wait until the end of the loop, you may wind up with a complex number that is too big for Python to represent!

Make sure that you are using return False somewhere inside your loop. You will want to return True after the loop has finished all of its iterations!


Check your inMSet function by copying and pasting these examples:

... either as assert tests: 

assert inMSet(0 + 0j, 25) == True
assert inMSet(3 + 4j, 25) == False
assert inMSet(.3 + -.5j, 25) == True
assert inMSet(-.7 + .3j, 25) == False
assert inMSet(.42 + .2j, 25) == True
assert inMSet(.42 + .2j, 50) == False
With thanks to Francine W. (CS5 '20!) for these!


... or individually at the command line: 


In [1]: c = 0 + 0j          # this one is in the set

In [2]: inMSet(c, 25)
Out[2]: True

In [3]: c = 3 + 4j          # this one is NOT in the set
# WARNING: this one might freeze or crash Python UNLESS your function
# returns False *as soon as* the magnitude is larger than 2.
# In other words, you need to return False _inside_ the loop
# (inside your if or your else, whichever is appropriate)!

In [4]: inMSet(c, 25)
False

In [5]: c = 0.3 + -0.5j     # this one is also in the set

In [6]: inMSet(c, 25)
Out[6]: True

In [7]: c = -0.7 + 0.3j     # this one is NOT in the set

In [8]: inMSet(c, 25)
Out[8]: False


In [9]: c = 0.42 + 0.2j

In [10]: inMSet(c, 25)      # this one _seems_ to be in the set
Out[10]: True

In [11]: inMSet(c, 50)      # but at 50 tries, it turns out that it's not!
Out[11]: False

In [12]: inMSet(0.42 + 0.2j, 50)
Out[12]: False              # another way to check a constant

Getting too many Trues?

If so, you might be checking for abs(z) > 2 after the for loop finishes. Be sure to check inside the loop!

There is a subtle reason you need to check inside the loop:

Many values get so large so fast that they overflow the capacity of Python's floating-point numbers. When they do, they cease to obey greater-than / less-than relationships, and so the test will fail. The solution is to check whether the magnitude of z ever gets bigger than 2 inside the for loop, in which case you should immediately return False.

The return True, however, needs to stay outside the loop!

As the last example illustrates, when numbers are close to the boundary of the Mandelbrot set, many additional iterations may be needed to determine whether they escape. This is why it is so computationally intensive to build high-resolution images of the Mandelbrot set.


Creating PNG images in Python

Getting started

Try out this code to get started: 

from cs5png3 import *   # You might already have this line at the top...

def weWantThisPixel(col, row):
    """This function returns True if we want to show
       the pixel at col, row and False otherwise.
    """
    if col % 10 == 0  and  row % 10 == 0:
        return True
    else:
        return False

def test():
    """This function demonstrates how
       to create and save a PNG image.
    """
    width = 300
    height = 200
    image = PNGImage(width, height)

    # Create a loop that will draw some pixels.

    for col in range(width):
        for row in range(height):
            if weWantThisPixel(col, row):
                image.plotPoint(col, row)

    # We looped through every image pixel; we now write the file.

    image.saveFile()

Save this code, and then run it by typing test()—with the parentheses—at the Python shell.


Windows users!  

End of the "DLL Error" warning that sometimes happens on Windows.


If everything goes well, test() will run through the nested loops and print a message that the file test.png has been created. That file should appear in the same directory as your hw8pr1.py file.

Live-updating image viewers for each OS:

(Another Windows alternative for live-updating is opening it in a browser... .)


Either way, for the above function, your image should be all white except for a regular, sparse point field, plotted wherever the row number and column number were both multiples of 10:

By the way, you can zoom in and out of images with the menu options or shortcuts. You might find that useful later when you're working with the actual Mandelbrot set.


Thought experiment:   and vs. or in pixel plotting

Before changing the above code, write a short comment under the test function in your hw8pr1.py file describing how the image would change if you changed the line 

if col % 10 == 0 and row % 10 == 0:
to the line 
if col % 10 == 0 or row % 10 == 0:

Then, make that change from and to or and try it. On both Macs and PCs, the image does not have to be re-opened: if you leave the previous image window open, its image will update automatically.

Just for practice, you might try creating other patterns in your image by changing the test and weWantThisPixel functions appropriately.



Some notes on how the test function works...

There are three lines of the test function that warrant a closer look:



From pixel coordinates to complex coordinates

The problem

Ultimately, we need to plot the Mandelbrot set within the complex plane. However, when we plot points in the image, we must manipulate pixels in their own coordinate system.

As the testImage() example shows, pixel coordinates start at (0, 0) (in the lower left) and grow to (width-1, height-1) in the upper right. In the example above, width was 300 and height was 200, giving us a small-ish image that will render quickly.

The Mandelbrot Set, as the image below shows, lives in the box
-2.0 ≤ x (or real coordinate) ≤ +1.0
and
-1.0 ≤ y (or imaginary coordinate) ≤ +1.0
which is a 3.0 x 2.0 rectangle.

So, we need to convert from each pixel's col integer value to a floating-point value, x. We also need to convert from each pixel's row integer value to the appropriate floating-point value, y.

An image of these relationships:

mset_geom.png


The solution

One function, named scale, will convert coordinates in general.

So, you'll next write this scale function: 

scale(pix, pixMax, floatMin, floatMax)
that can be run as follows: 
In [1]: scale(150, 200, -1.0, 1.0)
Out[1]: 0.5
Here, the arguments mean the following: Finally, the return value should be the floating-point value that corresponds to the integer pixel value of the first argument.

The return value will always be somewhere between floatMin and floatMax (inclusive).

This function will NOT use a loop. In fact, it's really just arithmetic. You will need to ask yourself:


Writing the scale function

To compute this conversion back and forth from pixel coordinates to complex coordinates, write a function that starts as follows: 

def scale(pix, pixMax, floatMin, floatMax):
    """scale accepts
           pix, the CURRENT pixel column (or row).
           pixMax, the total number of pixel columns.
           floatMin, the minimum floating-point value.
           floatMax, the maximum floating-point value.
       scale returns the floating-point value that
           corresponds to pix.
    """
The docstring describes the arguments: Note that there is no pixMin because the pixel count always starts at 0.

Again, the idea is that scale will return the floating-point value between floatMin and floatMax that corresponds to the position of the pixel pix, which is somewhere between 0 and pixMax. This diagram illustrates the geometry of these values:

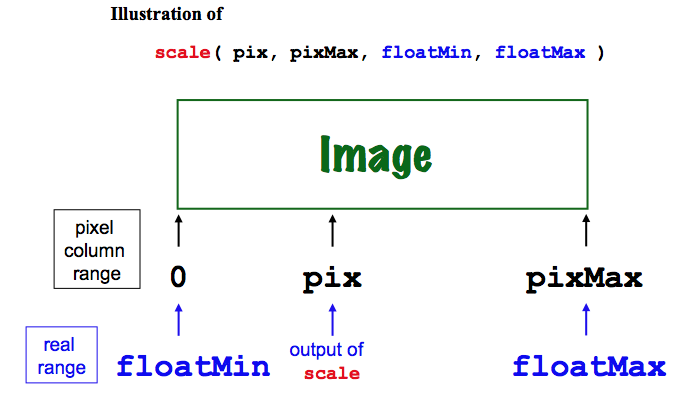
Once you have written your scale function, here are some test cases to try to be sure it is working: 

In [1]: scale(100, 200, -2.0, 1.0)  # Halfway from -2 to 1 should be -0.5
Out[1]: -0.5

In [2]: scale(100, 200, -1.5, 1.5)  # Halfway from -1.5 to 1.5 should be 0.0
Out[2]: 0.0

In [3]: scale(100, 300, -2.0, 1.0)  # 1/3 of the way from -2 to 1 should be -1.0
Out[3]: -1.0

In [4]: scale(25, 300, -2.0, 1.0)   # 1/12 of the way from -2 to 1 should be -1.75
Out[4]: -1.75

In [5]: scale(299, 300, -2.0, 1.0)  # Your exact value may differ slightly...
Out[5]: 0.99

Note Although we initially described scale as computing x-coordinate (real-axis) floating-point values, your scale function works equally well for both the x- and the y-dimensions. You don't need a separate function for the vertical axis!


Visualizing the Mandelbrot set in black and white: mset

This part asks you to put the pieces from the above sections together into a function named mset() that computes the set of points in the Mandelbrot set on the complex plane and creates a bitmap of them, of size width by height.

x and y ranges

To focus on the interesting part of the complex plane, we will limit the ranges of x and y to

-2.0 ≤ x or real coordinate ≤ +1.0
    and
-1.0 ≤ y or imaginary coordinate ≤ +1.0

which is a 3.0 x 2.0 rectangle.

Reprise of picture:

mset_geom.png


How to get started?    Start by copying the code from the test function and renaming it as mset: 

def mset():
    """Creates a 300x200 image of the Mandelbrot set.
    """
    width = 300*1       # We can update the 1 later to enlarge the image...
    height = 200*1
    image = PNGImage(width, height)

    # Create a loop to draw some pixels

    for col in range(width):
        for row in range(height):
            # Use scale twice:
            #   once to create the real part of c (x)
            # x = scale( ..., ..., ..., ...)
            #   once to create the imaginary part of c (y)
            # y = scale( ..., ..., ..., ...)
            # THEN, create c, choose n, and test:
            c = x + y*1j
            n = 25
            if inMSet(c, n) == True:
                image.plotPoint(col, row)

    # We looped through every image pixel; we now write the file
    image.saveFile()

(Note: in the above code we wrote "if inMSet(c, n) == True:" to make it clear what we're doing. Experienced programmers would usually write just "if inMSet(c, n):", which accomplishes the same thing. Why does this work? And why is it preferred style?)

To build the Mandelbrot set, you will need to change a number of behaviors in this function—start where the comment suggests that you should Use scale twice:

Once you've composed your function, try 

In [1]:  mset()
and check to be sure that the image you get is a black-and-white version of the Mandelbrot set, e.g., something like this:

Distorted? Rotated? Check to be sure you haven't mixed up x and y!


Adding features to your mset function

Changing colors...

You don't have to use just black and white!

The image.plotPoint method accepts an optional third argument that represents the color of the point you'd like to plot. Here is an example: 

image.plotPoint(col, row, (0, 0, 255))
The third argument here is a list that uses parentheses instead of square brackets. Parenthesized lists are called tuples in Python. Tuples are faster to access than lists, but their elements cannot be assigned to, so they're often used for constants such as colors.

The three elements of the color tuple above are red, then green, then blue; each of those three color components must be an integer from 0 to 255. Thus, the tuple above, (0, 0, 255) is pure blue.

To change the background of the set, add the lines 

else:
    image.plotPoint(col,row, (0, 0, 0))

within the loops that run over each col and each row. This will explicitly plot, in black, all of the points not in the Mandelbrot Set


Try it out! perhaps first by changing your Mandelbrot set to orange (255, 175, 0) on top of a black background (0, 0, 0).

Then, change the colors to something more to your liking!

Feel free to enlarge your image, too—it will take longer to render, but you'll be able to resolve more detail in the result!


Too slow? Note that inside the "inner" loop, col never changes. But you're calling scale to calculate x every time. How could you change the code so that you calculate x only when col changes? (Hint: No extra code is needed.)


No magic numbers!

Magic Numbers are simply literal numeric values that you have typed into your code. They're called magic numbers because if someone tries to read your code, the values and purpose of those numbers seem to have been "pulled out of a hat."

To keep your code as flexible and expandable as possible, it's a good idea to avoid using these "magic numbers" for important quantities in various places in your functions. Instead, it's better to collect all of those magic numbers at the very top of your functions (after the docstring) and to give them useful names that suggest their purpose. It's common, though not required, to use only capital letters for these values.

In addition to being clearer, this makes it much easier to add or change functionality in your code—all of the important quantities are defined one time and in one place.

For this part of the lab, move all of your magic numbers to the top of the function and give them descriptive names. For example, these five lines are a good starting point: 

NUM_ITERATIONS = 25  # Number of updates; will be assigned to n
XMIN = -2.0          # The smallest real coordinate value
XMAX =  1.0          # The largest real coordinate value
YMIN = -1.0          # The smallest imaginary coordinate value
YMAX =  1.0          # The largest imaginary coordinate value

These variables can then be changed in one place if you want to alter the "window" onto the Mandelbrot set being plotted.

In the next part, you'll change these values to zoom into the Mandelbrot set.


Zooming in!

For this part, simply run your mset function with some different values of XMAX, XMIN, YMAX, and YMIN to create images of different parts of the Mandelbrot Set.

Here is an example that uses 

    NUM_ITERATIONS = 100  # of updates
    XMIN = -1.2  # The smallest real coordinate value
    XMAX =  -.6  # The largest real coordinate value
    YMIN = -.5   # The smallest imaginary coordinate value
    YMAX = -.01  # The largest imaginary coordinate value
    FACTOR = 3
    width = 300*FACTOR
    height = 200*FACTOR
    image = PNGImage(width, height)   # make sure the image is the correct size!

test_michelle_lum_19.png

with acknowledgments and thanks to Michelle Lum, in CS5 in '19, whose code was used here!

Just for the record, the above image used these values: 

    NUM_ITERATIONS = 100  # of updates
    XMIN = -1.2  # The smallest real coordinate value
    XMAX =  -.6  # The largest real coordinate value
    YMIN = -.5   # The smallest imaginary coordinate value
    YMAX = -.01  # The largest imaginary coordinate value
    FACTOR = 3
    width = 300*FACTOR
    height = 200*FACTOR
    image = PNGImage(width, height)  # make sure the image is the right size


Another range you're welcome to try is amidst the "infinite snowmen": 

    NUMITER = 25
    XMIN = -1.2
    XMAX = -.6
    YMIN = -.5
    YMAX = -.1

Optionally, feel free to look around to find another set of values that shows an interesting piece of the set—and note what they are in a comment in your hw8pr1.py file. As a guide, you might consider the suggestions at this page on the "Seahorse Valley".

Note that the aspect ratio of the image is 3:2 (horizontal:vertical), and if you keep this aspect ratio in your ranges, the set will be scaled naturally.

It will work with different ratios, but to maintain the natural scaling, you would have to change the height and width of the image accordingly. Or you could compute the height and width, but that's not required for this lab.


Sounds

The Mandelbrot set is infinitely interesting…and in fact you can do more than just make pictures with it. Feel free to explore on the Internets!


Complete!

You've completed Lab #8 and built your own Mandelbrot Set!

Be sure to submit your hw8pr1.py to the usual spot on this week's homework...

Also welcome are any and all screenshots you're willing to share!


There are more directions to go, for sure, but they're 100% optional.

If you'd like to visualize the different escape velocities or change the resolution or perhaps mandelbrotify another image, these next sections describe how to add features to your Mandelbrot-set program. They're optional, but fun!



Completely Optional: Visualizing escape velocities

These extensions are optional (but fun!)—this first one lets you see the relative speeds with which the points in and around the Mandelbrot set escape to infinity.


Images of fractals often use color to represent how fast points are diverging toward infinity when they are not contained in the fractal itself. For this problem, create a new version of mset called msetColor . Simply copy and paste your old code, because its basic behavior will be the same. However, you should alter the msetColor function so that it plots points that escape to infinity more quickly in different colors.

The idea is to have your msetColor function plot the Mandelbrot set as before. In addition, however, use at least three different colors to show how quickly points outside the set are diverging—this is their "escape velocity." Making this change will require a change to your inMSet helper function, as well. We suggest that you copy, paste, and rename inMSet so that you can change the new version without affecting the old one.

There are several ways to measure the "escape velocity" of a particular point. One is to look at the resulting magnitude after the iterative updates. Another is to count the number of iterations required before it "escapes" to a magnitude that is greater then 2. An advantage of the latter approach is that there are fewer different escape velocities to deal with.

Choose one of those approaches—or design another of your own—to implement msetColor.


Two examples—entirely grayscale, admittedly! smile )

escape2.png   escape1.png


Mandelbrotifying another image

The png library can read images, too. (As a warning, it's not overly fast in converting them to Python lists…)

The result is that you can use another image's pixels to determine the look of the points in (or out of) your Mandelbrot set, e.g.,

Here is an example function to show how to read in an image (the alien.png image from the pngs folder: 

def example():
    """Shows how to access the pixels of another png image.

       inputPixels will be a list of rows, 
           each of which is a list of columns,
           each of which is a list [r,g,b].
    """

    iP = getRGB("./pngs/alien.png")
    inputPixels = []
    for row in iP[::-1]:             # The rows are reversed
        # convert to our format (not worth worrying about)
        inputPixels += [[ px[0][:-1] for px in row ]]  

    height = len(inputPixels)
    width = len(inputPixels[0])
    image = PNGImage(width, height)

    for col in range(width):
        for row in range(height):
            if col%10 < 5 and row%10 < 5: # Only plot some of the pixels
                image.plotPoint(col, row, inputPixels[row][col])

    image.saveFile()

The above code produces the following image:

Try Mandebrotifying this image—or another png you'd like to use…



When you are done—and it can be surprisingly addictive—you are done with lab!

Be sure to submit your hw8pr1.py file ...