The cost of a program's execution
(running time, memory, ...)
rather than
The cost of the program
(# of statements, development time)
[In this sense, less-complex programs require more development time.]
We focus primarily on running
time as
the measure of complexity.
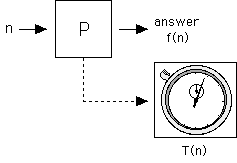
Consider a program with one natural number as input.
Two functions that can be associated with the program are:
(1) The function computed by the program -- f(n)
(2) The running time of the program -- T(n)

However, it is customary to measure T based on the "size" of the input,
rather than the input value.
Other size measures are
also used
e.g. for an array computation the size of the array might be used,
ignoring the fact that the numbers stored in the array have different lengths.
In a finer-grained analysis, these lengths would need to be taken into account.
Primitive Operations
These are operations which we don't further decompose.
They are considered the fundamental building blocks of the algorithm.
+ * - / if( )
Typically, the time they take is assumed to be constant.
This assumption is not always valid.
In doing arithmetic on arbitrarily-large numbers, the size of the numerals representing those numbers has a definite effect on the time required.
2 x 2
vs.
263784915623 x 78643125890
For a single number (n) input, size is typically on the order of log(n)
e.g. decimal encoding:
size(n) = #digits of n
= Ïlog10n¸
Ïx¸ = smallest integer > x
(called the ceiling of x)
The base
of the log, or radix of encoding, is not too important,
since log functions differ only by constant factors :
logb(x) = logc(x) / logc(b)
(logb(x) and logc(x) have two different bases, and logc(b) is a constant)
e.g.
log2(x) = log10(x) / log10(2)
log10(2) = 0.30103
1 / 0.30103 = 3.32193
When we write "log" it is usually log2 by default.
Unless we state otherwise, we'll assume constant costs for
+ , * , / , < , etc.
We will further approximate that all take the same time, which we'll call
1 "step"
The time of a step varies among computers.
But the number of steps will be the same for a given program.
Counting Steps
Straight-Line Code:
Loop-Code:
Steps are a function of # of iterations
Recursive Code:
Steps can be determined by solving recurrence
Recurrence for run-time T:
The recurrence
T(0) => 1;
T(n+1) => 1 + T(n);
has the solution
T(n) = n + 1
One way to see this is by repeated substitution:
Recursive Code can sometimes be analyzed by understanding the number
of recursive cells, then multiplying that number by an appropriate
factor.
In both loops and recursion, the number of cells/iterations is not always obvious.
Example
while loop, lists
List L;
L = ... ;
while ( !empty(L) )
{
:
:
L = rest(L);
}The multiplying factor (# of iterations) is the length of the list.
"O" (order) notation
expresses upper bound on execution time to within a constant factor
[ For other than natural number args, this definition is inadequate. ]
°[ sometimes T=O(f) is used ]
Example
T(n) = 1.5 n2
f(n) = n2
T
O(f)
since by taking c=1.5
we have
We could also use anonymous
fns :
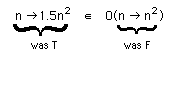
We usually abbreviate this by dropping one or both n Æ :
T  O(1) means T is upper bounded by a constant
O(1) means T is upper bounded by a constant
![]()
We say "O(1)" when we mean some constant (not a function of input)
Linear-Addressing Principle
Any access to memory is O(1).
Typical algorithm growth rates
O(n) ("linear")
finding the max in an array
O(n2) ("quadratic")
Sorting an array by a naive method
Example
O(log n) algorithm
Binary Search
There are O(log n) steps.
Each step is O(1), due to linear addressing principle.
O(log n) overall
log n
grows so slowly, it is "almost" as good
as a constant:
Doubling n only adds 1 to log n.
Doubling n doubles n.
log arises in a recurrence of form
T(1)
0;
T(2*n)
T(n) + 1;
solution: T(n) = Ïlog n¸
To see this, use repeated substitution:
O(n log n)
Sorting an array by an optimal method
n log n is better than n2 :
Divide each by the factor n
Scalability Considerations
O notation focuses on comoparing "growth rate" of functions:
T
O( n2 )
means T(n) grows no faster than n2 grows.
This is useful in comparing algorithms; it gives us an idea about how well the algorithm performs over an infinite range of inputs.
2 algorithms for some problem
Algorithm A has a preferable growth rate (O(n)) compared to algorithm B (O(n2)),
even though A is worse than B in some finite range.
Polynomial-time algorithms are preferred over non-polynomial
Some problems are not known to possess any polynomial-time algorithm.
[Some are also not known not to possess a polynomial-time algorithm.]
Examples
Checking whether an arbitrary SOP form is a tautology.
Traveling salesperson problem
TSP (Traveling Salesperson Problem)
Given n cities with costs between each pair, find the "tour" which minimizes total cost.
Tour = permutation of cities
There are n! possible tours
obvious method is O(n!)
Tautology-Checking
Could use Boole-Shannon expansion:
Tree of height n (= # vars)
2n leaves
O(2n) is bound for this algorithm