Problem C
Kissin' Cousins

The Oxford English Dictionary defines cousin as follows:
cous'in (k\O(u,ù)zn), n. (Also first cousin) child of one's uncle or aunt; my second (third...) cousin, my parent's first (second...) cousin's child; my first cousin once (twice...) removed, my first cousin's child (grandchild...), also my parent's (grandparent's...) first cousin.

Put more precisely, any two persons whose closest common ancestor is (m+1) generations away from one person and (m+1)+n generations away from the other are mth cousins nce removed. Normally, m >= 1 and n >= 0, but being used to computers counting from 0, in this problem we require m >= 0 and n >= 0. This extends the normal definition so that siblings are zeroth cousins. We write such a relationship as cousin-m-n.

If one of the persons is an ancestor of the other, p generations away where p >= 1, they have a relationship descendant-p.

A relationship cousin-m1-n1 is closer than a relationship cousin-m2-n2 if m1 < m2 or (m1 = m2 and n1 < n2). A relationship descendant-p1 is closer than a relationship descendant-p2 if p1 < p2. A descendant-p relationship is always closer than a cousin-m-n relationship.

Write a program that accepts definitions of simple relationships between individuals and displays the closest cousin or descendant relationship, if any, which exists between arbitrary pairs of individuals.

Input

Each line in the input begins with one of the characters '#', 'R', 'F' or 'E'.

'#' lines are comments. Ignore them.

'R' lines direct your program to record a relationship between two different individuals. The first 5 characters following the 'R' constitute the name of the first person; the next 5 characters constitute the name of the second. Case is significant. Following the names, possibly separated from them by blanks, is a non-negative integer, k, defining the relationship. If k is 0, then the named individuals are siblings. If k is 1, then the first named person is a child of the second. If k is 2, then the first named person is a grandchild of the second, and so forth. Ignore anything on the line following the integer.

'F' lines are queries; your program is to find the closest relationship, if any, which exists between the two different persons whose 5 character names follow the 'F'. Ignore anything on the line following the second name. A query should be answered only with regard to 'R' lines which precede the query in the input.

There will be one 'E' line to mark the end of the input data. Ignore anything on or after the 'E' line.

Output

For each 'F' line, your program is to report the closest relationship that exists between the two persons named aaaaa and bbbbb in one of the following formats:
aaaaa and bbbbb are descendant-p.
aaaaa and bbbbb are cousin-m-n.
with m, n and p replaced by integers calculated as defined above. If no relationship exists between the pair, your program is to output the following:
aaaaa and bbbbb are not related.

Assumption:
A person is not an ancestor of himself/herself.

Sample Input 

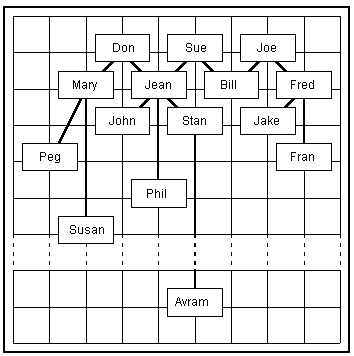
# A Comment!
RFred Joe  1 Fred is Joe's son
RFran Fred 2
RJake Fred 1
RBill Joe  1
RBill Sue  1
RJean Sue  1
RJean Don  1
RPhil Jean 3
RStan Jean 1
RJohn Jean 1
RMary Don  1
RSusanMary 4
RPeg  Mary 2
FFred Joe
FJean Jake
FPhil Bill
FPhil Susan
FJake Bill
FDon  Sue
FStan John
FPeg  John
RAvramStan  99
FJean Susan
E

Output for the Sample Input

Fred  and Joe   are descendant-1.
Jean  and Jake  are not related.
Phil  and Bill  are cousin-0-3.
Phil  and Susan are cousin-3-1.
Jake  and Bill  are cousin-0-1.
Don   and Sue   are not related.
Stan  and John  are cousin-0-0.
Peg   and John  are cousin-1-1.
Jean  and Susan are cousin-0-4.

Diagram of the Sample Input