Cow Toll Paths 

Like everyone else, FJ is always thinking up ways to increase his
revenue. To this end, he has set up a series of tolls that the cows
will pay when they traverse the cowpaths throughout the farm.

The cows move from any of the N (1 <= N <= 250) pastures conveniently
numbered 1..N to any other pasture over a set of M (1 <= M <= 10,000)
bidirectional cowpaths that connect pairs of different pastures A_j
and B_j (1 <= A_j <= N; 1 <= B_j <= N). FJ has assigned a toll L_j
(1 <= L_j <= 100,000) to the path connecting pastures A_j and B_j.

While there may be multiple cowpaths connecting the same pair of
pastures, a cowpath will never connect a pasture to itself.  Best
of all, a cow can always move from any one pasture to any other
pasture by following some sequence of cowpaths.

In an act that can only be described as greedy, FJ has also assigned a
toll C_i (1 <= C_i <= 100,000) to every pasture. The cost of moving
from one pasture to some different pasture is the sum of the tolls
for each of the cowpaths that were traversed plus a *single additional
toll* that is the maximum of all the pasture tolls encountered along
the way, including the initial and destination pastures.

The patient cows wish to investigate their options. They want you
to write a program that accepts K (1 <= K <= 10,000) queries and
outputs the minimum cost of trip specified by each query. Query i
is a pair of numbers s_i and t_i (1 <= s_i <= N; 1 <= t_i <= N; s_i !=
t_i) specifying a starting and ending pasture.

Consider this example diagram with five pastures:











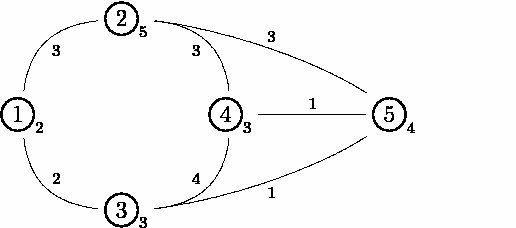
The 'edge toll' for the path from pasture 1 to pasture 2 is 3.
Pasture 2's 'node toll' is 5.

To travel from pasture 1 to pasture 4, traverse pastures 1 to 3 to
5 to 4. This incurs an edge toll of 2+1+1=4 and a node toll of 4
(since pasture 5's toll is greatest), for a total cost of 4+4=8.

The best way to travel from pasture 2 to pasture 3 is to traverse
pastures 2 to 5 to 3. This incurs an edge toll of 3+1=4 and a node
toll of 5, for a total cost of 4+5=9.

PROBLEM NAME: toll

INPUT FORMAT:

* Line 1: Three space separated integers: N, M, and K

* Lines 2..N+1: Line i+1 contains a single integer: C_i

* Lines N+2..N+M+1: Line j+N+1 contains three space separated
        integers: A_j, B_j, and L_j

* Lines N+M+2..N+M+K+1: Line i+N+M+1 specifies query i using two
        space-separated integers: s_i and  t_i

SAMPLE INPUT:

5 7 2
2
5
3
3
4
1 2 3
1 3 2
2 5 3
5 3 1
5 4 1
2 4 3
3 4 4
1 4
2 3

OUTPUT FORMAT:

* Lines 1..K: Line i contains a single integer which is the lowest
        cost of any route from s_i to t_i

SAMPLE OUTPUT:

8
9