Problem B: Advanced Causal Measurements (ACM)
Causality is a very important concept in theoretical physics. The
basic elements in a discussion of causality are events. An
event e is described by its time of occurrence t, and
its location, x, and we write e =
(t,x). For our concerns, all events happen
in the one dimensional geometric space and thus locations are given by
a single real number x as a coordinate on x-axis.
Usually, theoretical physicists like to define the speed of light to
be 1, so that time and space have the same units (actual physical
units frighten and confuse theorists).
One event e1 =
(t1,x1) is a possible
cause for a second event e2 =
(t2,x2) if a signal
emitted at e1 could arrive at
e2. Signals can't travel faster than the speed of
light, so this condition can be stated as:
e1 is a possible cause for e2
iff
t2 >= t1+|x2-x1|
Thus an event at (-1,1) could cause events at (0,0), (1,2), and (1,3),
for example, but could not have caused events at (1,4) or (-2,1).
Note that one event can cause several others.
 Recently, scientists have observed several unusual events in the
geometrically one dimensional universe, and using current theories,
they know how many causes were responsible for these observations, but
they know nothing about the time and space coordinates of the causes.
You asked to write a program to determine the latest time at which the
earliest cause could have occurred (i.e. the time such that at least
one cause must have occurred on or before this time). Somewhat
surprisingly, all the observed events have both space and time
coordinates expressed by integer numbers in the range
-1000000 ≤ t, x ≤ 1000000.
Recently, scientists have observed several unusual events in the
geometrically one dimensional universe, and using current theories,
they know how many causes were responsible for these observations, but
they know nothing about the time and space coordinates of the causes.
You asked to write a program to determine the latest time at which the
earliest cause could have occurred (i.e. the time such that at least
one cause must have occurred on or before this time). Somewhat
surprisingly, all the observed events have both space and time
coordinates expressed by integer numbers in the range
-1000000 ≤ t, x ≤ 1000000.
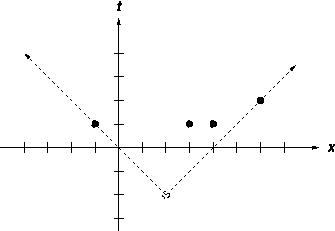
The figure on the right illustrates the first case from input: the earliest
single event as a possible cause of all four events.
The first line of input is the number of cases which follow. Each
case begins with a line containing the number n of events and
the number m of causes,
1 ≤ n, m ≤ 100000. Next
follows n lines containing the t and x
coordinates for each event.
Output consists of a single line for each case in the format as in the
sample output, giving the latest time at which the earliest
cause could have occurred, this will be an integer as our time units
are not divisible.
Sample Input
4
4 1
1 -1
1 3
1 4
2 6
4 2
1 -1
1 3
1 4
2 6
4 3
1 -1
1 3
1 4
2 6
4 4
1 -1
1 3
1 4
2 6
Output for Sample Input
Case 1: -2
Case 2: 0
Case 3: 0
Case 4: 1
Daniel Robbins
 Recently, scientists have observed several unusual events in the
geometrically one dimensional universe, and using current theories,
they know how many causes were responsible for these observations, but
they know nothing about the time and space coordinates of the causes.
You asked to write a program to determine the latest time at which the
earliest cause could have occurred (i.e. the time such that at least
one cause must have occurred on or before this time). Somewhat
surprisingly, all the observed events have both space and time
coordinates expressed by integer numbers in the range
-1000000 ≤ t, x ≤ 1000000.
Recently, scientists have observed several unusual events in the
geometrically one dimensional universe, and using current theories,
they know how many causes were responsible for these observations, but
they know nothing about the time and space coordinates of the causes.
You asked to write a program to determine the latest time at which the
earliest cause could have occurred (i.e. the time such that at least
one cause must have occurred on or before this time). Somewhat
surprisingly, all the observed events have both space and time
coordinates expressed by integer numbers in the range
-1000000 ≤ t, x ≤ 1000000.