Southeastern European Regional Programming Contest  Bucharest, Romania  October 23, 1999

Problem E
Topographic Map

source file:   topo.cc

Consider an abstraction of a map as a two dimensional grid of points enclosed within a rectangular contour. The boundary of the map and the obstacles on the map are marked using the character 'X' .  The free points on the map are marked by characters corresponding to decimal digits. In addition, there are precisely two distinct towns on the map, marked using the letters A and B.

Now, each digit on the map represents the altitude of the region that digit represents. The units are tens of meters, so that (in meters) the altitude of a point p is 10*digit(p) if digit(p) is the digit corresponding to point p on the map. You may assume that the two towns are at sea level, i.e., altitude(A)=altitude(B)=0.  In order to get around this region you have access to an unusual vehicle: a car which can be started at town A at any (integral) velocity you like, but whose speed is otherwise at the mercy of the hills and valleys of the countryside. This car can move one space at a time (on the map) -- vertically, horizontally, and diagonally, and only through the free points (digits). The vehicle must have a strictly positive speed during its journey, except for at the goal point B where its speed can be 0.

When the vehicle advances from a point p to a neighbouring point q, it's speed is reduced by 1 meter per second because of energy losses due to friction. In addition, the vehicle changes by (altitude(p) - altitude(q)) meters per second because of the change in height of the road. Note that this change might
be positive (in the case that p was higher than q) or negative (if q is higher than p).

Thus, the speed at point q, having moved from a neighboring point p, is

speed(q) = speed(p) + altitude(p) - altitude(q) - 1
 

The problem

1. The minimum initial speed (Vmin) the vehicle must have, when it departs from A, for being able to reach B.

2. The maximum final speed (Vmax) the vehicle can have when it reaches B, after departing from A with the speed Vmin.
 

Input Format

Output Format

For each map the program prints to the standard output, on a separate line, the pair of values Vmin , Vmax .  These values should be separated by a comma and a single space. If the vehicle cannot reach B the message "No solution" should be printed.
 

Examples

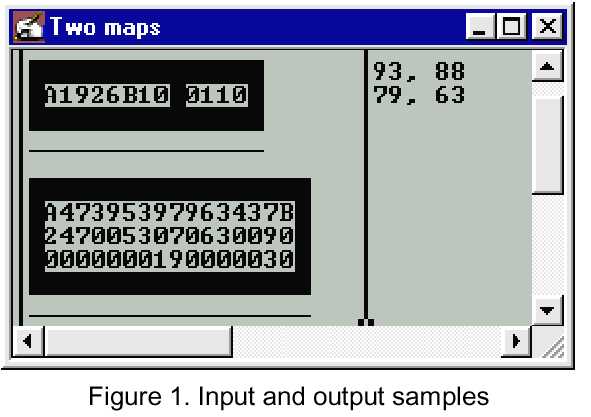
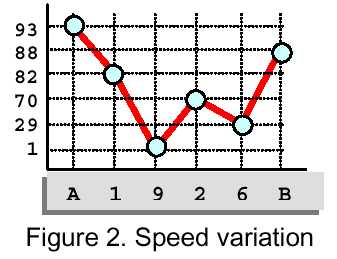
Figure 1  illustrates samples of program input and output (don't worry about the fact that this is done in windows or that the 'X' characters are solid blocks...) Figure 2 shows the vehicle speed variation for the first map from figure 1. Figure 3 displays a possible path followed by a vehicle with Vmin =79 and Vmax =63 on the second map from Figure 1.