Zeke Burgess, Bryce Nichols, Ronalee Lo

Computer Science 154- Robotics

Lab 1

The Manipulator

 

 

Introduction

            This lab combined the use of robotic control, manipulation, and fortune telling.  We were asked to design a robotic arm capable of divination with the aid of a Ouija Board.  In order for the robot to communicate with us, we will devise an algorithm that will translate Cartesian coordinates into Ouija character location coordinates.

 

Design

            The first task of building this robot soothsayer was to decide on a good design.  After experimenting with the different design possibilities that can be achieved from the wide assortment of connection pieces and six servo motors, we chose a design that used three motors.  This configuration was based on the "Draw-Bot" located on page 69 of the Robix Manual. We made some minor changes to accommodate our designed functionality. See fig. 1 for a picture of the robot configuration.

 

 

 

           

During the construction of the robot we noted our design would be affected if extraneous weight was added to the end of the arm.  When the arm was fully extended, the arm was incapable of supporting a large enough weight attached the end of the arm.  We decided to forgo the use of the gripping tool since it added a tremendous amount of weight to the arm, making the servos unhappy.  However, we needed a way to attach the Ouija Planchette to the arm.  A solution was to construct a 90° angle joint in the engineering sheet metal shop.  Another segment was then attached perpendicular to the arm.  We then attached a stack of Legos to the Planchette.  We then taped the Legos to the arm extension.

           

            We confirmed that this robot was capable of reaching the entire usable area of the Ouija Board by using the manual controls to move the arm to the farthest points on the board.  We then performed a series of tests to see how accurately we could model the position of the robot.  The robot had could reach any point within a 180° arc with the radius of the arm, except points extremely close to its base.  We found that the robot had many limitations, such as each servo does not necessarily rotate 90° to the left and right, see fig. 2.  However, each of these anomalies were repeatable so we can introduce a correction factor into our equations to account for errors.

 

 

 

 

The Kinematics

            The next task is to give the robot enough information about it environment, as well as an algorithm capable of translating the environment into data the robot can use, for it to move to a letter of it's choosing. 

 

 

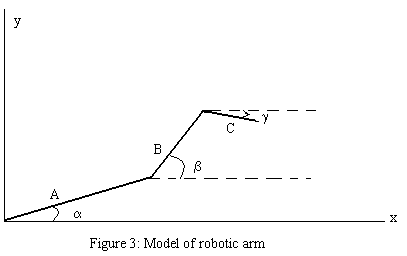
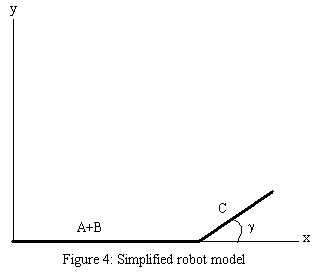
We noted that the robot could reach all of the letters location on the Ouija Board by only moving two of its servos.  We were able to simplify our model of the robot, and subsequently the kinematics equations.  Figure 3 is a model of the actual robot and fig. 4 is the configuration we used to model motion in the robot.

 

 

            The robot needs an algorithm that can translate a variety of points in a 2D space (the Ouija Board)  into polar coordinates.  Polar coordinates are more useful to the robot because it controls the Ouija Planchette by moving each segment to a particular angle relative to another segment.  We figured out that the simplified model of the robot can reach all of the characters but not the numbers, however, a two segment robot arm has a simpler set of equations to those of a three segment robot arm.  Therefore, we will code an algorithm that will take a set of letters and calculate how to move the arm to the location of each letter.  However, the location of the numbers, "yes", "no", and "good bye" will be hardcoded for the robot (eventually, not as of this documents origin).

 

            The following equations were used to describe the location of the letters relative to the robot. 

 

            x = C * cos (a + b + g) + B * cos (a+b) + A * cos a

 

            y = C * sin (a + b + g) + B * sin (a+b) + A * sin a

 

            g = acos((16 * r^2 - 1325)/1276)

 

            a = theta - atan( C * sin g/(A + B + C * cos g))

 

 

 

 

            The 2D coordinate system to designate the location of each letter was measured and fed into a table for the robot to look up.  We picked a point on each letter and measured its location.  Each letter location is comprised of an x and y value, which was measured from the bottom right corner of the Oujia Board. 

 

            However, we also needed a way to decide what servo to move when and where.  This is the role of reverse kinematics.  Our solution uses a two-step method to find a letter.  First, it moves the third servo to the correct eventual distance from the origin.  The second step involved calculating the amount of rotation from the first servo.  With this method, we can easily locate any Cartesian point.