Reactive and low-level control
CS154, Spring 2002
Daniel Lowd
Part 1: Reactive control
Introduction
Early attempts at mobile robotics were dominated by model-building approaches
using the sense, plan, act (SPA) architecture [Gat]. Sensors were used to
build a model of the environment, an analytical engine planned a course,
and the resulting plan was used to drive the robot. Unfortunately, these
robots tended to be slow and unreliable. Building a world model was computationally
expensive and could get outdated as the plan was being constructed.
Reactive control was first suggested by Rodney Brooks, whose insect-like
robots demonstrated exceptional speed and robustness yet required very limited
computational power [Brooks89]. Instead of building a model, these robots
reacted to their environment, with higher-level behaviors overriding lower-level
ones as necessary to achieve more complex behavior.
Though inadequate for some tasks, responding directly to sensors can be
enough to achieve basic obstacle avoidance or wall-following behavior. My
goals for the first part of this project are to implement basic obstacle-avoidance
behaviors in the Nomad 200 robot.
Approach
Since the Nomad 200 is prebuilt and pretested, and has good software simulator
support, programming it is fairly straightforward. The basic locomotion
and control challenges that other robotics projects face [Phee02] are avoided
here by using a manufactured base. This leaves the challenge of directing
it based on sensor readings. To address this, I am implementing a reactive
control program for the Nomad 200. Rather than storing the state of the
world internally, this program will respond exclusively to its sonar sensors.
The Nomad is also equipped with radar for short-range sensing, as well
as contact bumpers. I avoid the use of these because I hope the robot will
avoid walls before getting too close to them. Furthermore, infrared sensors
may be affected by lighting conditions. By not depending on infrared, I
hope to achieve a more robust solution. The robot"s current translational
and rotational velocities are accessible, so it would be possible to react
to them as well as the environment. For a first trial implementation, I
will ignore these in hopes of a simpler, purer, though perhaps less effective
solution.
Progress
Development was done using a simulator. While simulation is no substitute
for the real world, it provided an easy and safe way to quickly test ideas.
As a starting point, I used the provided file survivor.cc and class discussions
of obstacle avoidance for developing my strategies. I chose to make
the robot turn towards the right or the left depending on how much space
there seemed to be in that direction, from the sensors. To accomplish this,
I simply set the rotational velocity to be the difference between the left
front and right front sensor ranges. This, however, would be insufficient
for avoiding a wall that was directly ahead. Corners could present
a similar challenge. To take care of this problem, I set a threshold
for the forward sensors. When a wall or object was detected closer than a
specified distance, the robot would turn left at a medium-high rotational
velocity. The threshold was tuned somewhat to achieve reasonable performance
in one test map.
The first implementation of this code actually turned left or right, depending
on which side seemed to have more space. I abandoned this, however, after
observing that the robot would crash into walls when ambivalent about direction.
Another approach is used in the sample solution to this problem: by reacting
to the current turn direction, an emergency avoidance turn may be maintained
in spite of inconsistent sensors.This may even work better than my solution,
but it depends on more information.
At my specified turning rate, the robot would still sometimes crash into
walls.Instead of increasing the turning rate, I decided to modify the robot’s
speed. I made the robot’s translational velocity proportional to the distance
detected by its forward sensors. This would give it plenty of time to turn
away from a wall when it got too close.The project page was unclear as to
whether modifying the translational velocity dynamically was permitted.Using
a greater rotational velocity would permit safe travel at reasonable speeds,
but seems less robust than this approach.
Below, I have included one sample run in the simulator. This program
has not yet been tested with other map files or in the real world, and may
yet need other modifications or parameter tuning. However, I believe
this suffices to show initial success. After achieving this, I switched
to focus on wall-following. I did not consider further refinement of
this part necessary, since successful wall-following will necessarily avoid
obstacles as well.
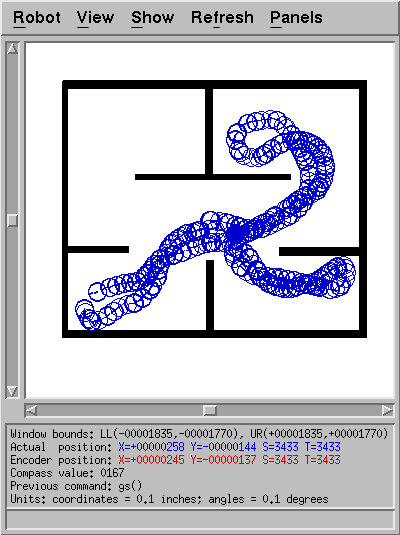
Figure 1: Sample run of obstacle avoidance code in the Nomad simulator.
Part 2: Wall-following
Introduction
Wall-following is a somewhat more sophisticated way to maneuver than simple
obstacle avoidance. Obstacle avoidance has as its only goal a lack
of collisions. One hopes that such an algorithm will also tend to explore
much of an area over time, but there are no guarantees. In contrast,
a wall-following algorithm may be used to reliably solve mazes or map out
areas. It also presents greater challenges; no longer is it sufficient
to run away from everything solid. A wall-following robot must maintain
a safe distance from all walls while never losing the one it follows.
A related problem is building a corridor-follower, a robot that maintains
an equal distance from each side of a hallway. Though this may be beneficial
in well-structured environments, it suffers in more chaotic ones. In
addition, the corridor-following problem is somewhat ambiguous: how does
one determine what is or is not a corridor in a complex environment? And
what should the robot do in the absence of clearly-defined corridors? Is
it a failure if a robot does not entirely fully explore an arbitrary yet
structured environment? Though not altogether unanswerable, these are
challenging questions with no one "right" answer.
For this project, I am avoiding those questions by focusing on wall-following,
a task that is, for the most part, well-defined. My performance goal
is to implement an algorithm for let Nomad 200 to maintain a constant distance
from walls while progressing at reasonably high speeds.
Initial Approach
I decided to look at wall-following as a control problem and implement
a PD controller to solve it. The goal is to maintain a certain distance
from either the left or right wall. I arbitrarily chose to follow
the right wall, though this does not affect the general approach. For
a measure of error, I decided to use the shortest distance to an object
on the right less the prespecified buffer distance (18 inches in my case).
This was then modified using information about which sensor had read
that closest reading. If the closest wall on the right is behind us,
then we should turn closer to the wall to maintain this same distance as
we proceed forward. On the other hand, if the closest wall is in front,
we should turn away to avoid getting closer. Specifically, the raw
error would be increased or decreased by as much as 40% based on which sensor
was being read.
I left in some of the original obstacle avoidance code, so that the robot
would slow down and take evasive maneuvers if it got too close to an object.
This code would only take effect when a wall was detected within 18
inches of the front sonars. The architecture used to tie these two
together was thus related to Brooks' subsumption architecture [Brooks89],
except that a lower-level behavior (obstacle-avoidance) is subsuming a slightly
higher-level behavior (wall-following), rather than letting higher-level
behaviors override lower-level ones.
Initial Results/Frustrations
I continued to use the simulator for both development and testing. While
I had some measure of success with following walls, it proved to be more
challenging than I had anticipated. I ran into two classes of problems.
If I made the gains too high, the robot would merely run in circles,
never finding a wall (Fig.2). If the gains were lowered too much,
the robot would follow walls more or less, but swing wide on corners (Fig.3).
I had some success with intermediate values, but even then the robot
would tend to weave somewhat (Fig.4). The robot's speed was fixed to
100 (10.0 in/sec) unless near a wall, at which point obstacle-avoidance behavior
slowed and turned the robot.

Figure 2: Sample run with excessively high gains. The robot gets
stuck in a loop because it never finds the wall.
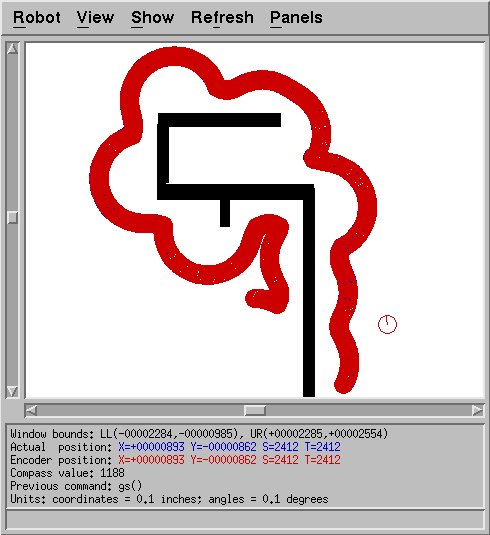
Figure 3: Sample run with insufficiently high gains. The result is
a failure to make tight turns around corners.
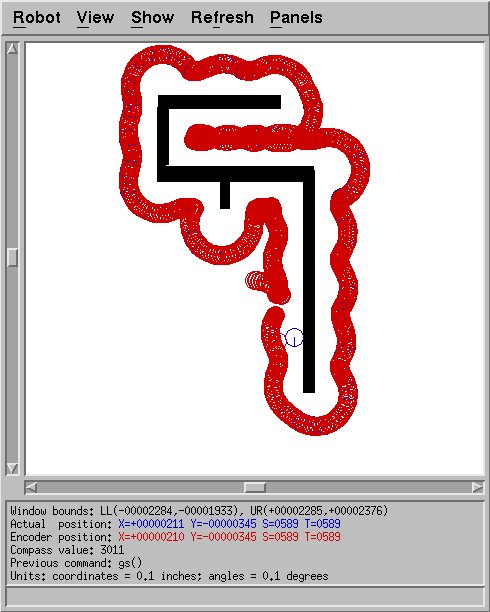
Figure 4: Sample run with intermediate gains. Corner turns are now
tighter, but the robot still weaves noticeably.
Revised Approach
Unsatisfied with these initial results, I used three strategies to improve
upon them. To correct the perpetual looping behavior of Fig.2, I implemented
a wall-seeking behavior. After being initialized, the robot goes straight
until its forward sensors detect a wall to follow; then its regular wall-seeking
behaviors take over for the remainder of its life. While it would be
possible to reenter this state, I never found that to be necessary. Once
the robot found a wall, it never lost it. In the real world, where walls
move and people look like walls, a more sophisticated wall-seeking behavior
would be appropriate. For my experiments in the simulator, this sufficed.
Once I had the wall-seeking behavior, I was free to use higher gains,
and thus achieve better cornering.
However, the robot still wove when it encountered a wall. My initial
obstacle-avoidance behavior had not been adequately modified to work with
the new goal of wall-following: as the robot approached a wall, its obstacle-avoidance
behavior took over to avoid the wall, but left it too close (fewer than 18
inches on the right). Since turning to avoid a corner was a common
occurrence, I developed a simpler approach: when a wall is too close in front,
stop going forward and turn.
Since some oscillation still remained, I improved my derivative calculation
to remember the past five errors rather than just the previous one. The
problem with remembering only the previous error is that sonar readings don't
necessarily change every timestep. By recording the last five errors,
I increased the probability that a slower change in error would be correctly
and consistently detected. One additional modification I had to make
was to clear the error history is cleared whenever the wall-avoidance code
takes over. Comparing errors before a turn with errors after a turn
led to incorrect behavior.
I initially implemented an integral term in my control algorithm, but never
found it necessary to use it. It seemed unlikely that there would be
a systematic error that an integral term would need to correct; the robot
never had trouble getting close enough to a wall or retreating away from it,
and the robot's situation varied too much to make an integral term of much
use.
Final Results
Using the described modifications, I was able to achieve very good wall-following,
even at high speeds (20.0 in/sec) with reasonable bounds on turning rates
(45.0 deg/sec). Fig.5 shows the result of my revised algorithm on a
challenging course.
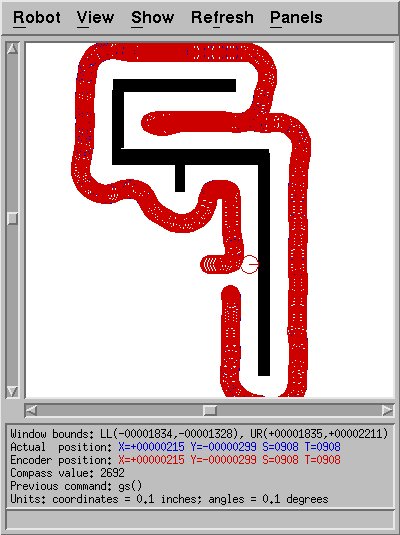
Figure 5: Sample run after algorithm enhancements; weaving is almost non-existent,
and overshooting is minimal.
The time had come for a challenge. Could the robot find its way out
of a large maze using this wall-following algorithm? I constructed
such a scenario, and after a couple of attempts, it succeeded. I first
had trouble because some of the corridors were too narrow: rather than passing
through, the robot would turn around and head for safety. By reducing
the wall-following distance from 18 inches to 12, I was able to help the
robot succeed without reconstructing the map from scratch. It should
be noted that some mazes with loops cannot be solved this way; this map was
specially constructed to be solveable by a wall-follower. Fig.6 documents
the attempt.
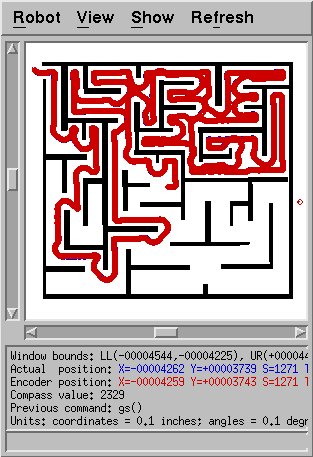
Figure 6: Successful escape from the maze. Base velocity was 20.0 in/sec.
One path was not followed because it was too narrow, but most others
were. Some overshooting is present; it might be possible to reduce
this with further parameter tuning.
One of the strengths of the wall-following method is that it can handle arbitrary
angles, not just square ones. Fig.7 shows the behavior of this algorithm
in an angled environment.

Figure 7: Sample run through a map with acute and obtuse angles.
Perspective
I have discovered and demonstrated a variety of strategies that yield successful
wall-following behavior in the Nomad simulator. Most novel was scaling
distance errors based on which sensor was responsible for the reading, so
that a close reading in front is treated differently from one behind. More
common techniques were using a PD controller for wall-following, and calculating
derivatives by storing the last several errors. The major successes
of this project are exceptionally smooth wall-following and minimal use of
state. Apart from storing the last several errors for calculating derivatives,
this algorithm uses only one bit of state: whether or not it has found a
wall. The rest is reactive control, with a subsumption-like override
for emergency wall-avoidance.
Some of the limitations of my work are that this is purely simulation and
that the algorithm required retuning for different environments. A
run in the real-world might reveal dependencies on ideal simulator conditions
which render certain approaches invalid. I already mentioned earlier
the possibility that the robot could lose the wall if the wall moved suddenly,
ending up in a confused circle as in Fig.2. Furthermore, I found it
necessary to retune the gains to achieve optimal performance on a given map.
With additional work and thought, a more robust algorithm might be
possible, perhaps utilizing machine learning techniques. One of the
clear issues with my algorithm is in the derivative calculation: I assume
that my sense/act loop takes a constant amount of time and thus that sensor
readings come at regular intervals. However, I have noticed that this
is not even the case in the simulator: sometimes it seems to run more slowly,
and other times more quickly. A stronger implementation would read
the system clock and take into account the actual time lapse rather than
assuming constancy.
A final issue is performance metrics: a more thorough review could report
average distances from the wall and use it as a metric for tuning and evaluating
algorithm performance. Lacking the time to thoroughly pursue metrics,
I evaluated my work qualitatively. The danger, of course, is that another's
evaluation might differ.
Supplementary Files
survivor1.cc: Source code for basic obstacle
avoidance. Based on survivor.cc base file, provided for class use.
survivor2.cc: Source code for wall-following,
also based on survivor.cc. Algorithm parameters are set within the
source code itself.
wallfollow_map_3: Wall-following test map
used for Figs 2-5.
maze1: Maze test map used for Fig 6.
Works Cited
- Brooks, Rodney. Achieving Artificial Intelligence through Building
Robots. A. I. Memo 899, Massachusetts Institute of Technology, Artificial
Intelligence Laboratory. 1986.
- Gat, Erann. On Three-Layer Architectures. In Artificial
Intelligence and Mobile Robots, Kortenkamp, Bonnasso, and Murphy,
eds., AAAI Press.
- Phee, L., A. Menciassi, S. Gorini, G. Pernorio, A. Arena, P. Dario.
An Innovative Locomotion Principle for Minirobots Moving in the
Gastrointestinal Tract. Proceedings of the 2002 IEEE International
Conference on Robotics & Automation. Washington, DC. May
2002.







