Project #2: Inverted Pendulum Robot

Matt Ferlo and Jordan Taggart

Introduction

Using the Evolution platform, we will make a robot capable of balancing an inverted pendulum. The pendulum will be constrained to rotate only about one axis. The Evolution's vision system will be used to track the pendulum, which will probably be painted an easily-distinguished color (much the same way that [Vaughan]'s sheep dog was distinctively painted).

Theory

There are two forces acting on the standing rod: gravity and the motion of the cart. This analysis assumes the "pendulum" is actually a rod with equal mass all along its length.

Gravity

Gravity acts all along the length of the beam, providing an equal force all along the beam.

F = ρ*L*g

where ρ is the linear density of the beam (mass per distance), L is the length of the beam, g is the acceleration of gravity, and a is the angle deviation from vertical.

This force provides a torque (T = Fperp*L where Fperp is the component of the force perpendicular to the beam, Fperp = F*sin(a)).

Tgravity = 0.5*ρ*L2*g*sin(a)


Cart Motion

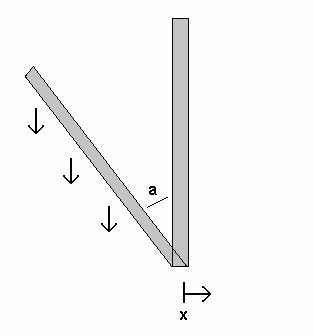
Independent of gravity, the motion of the cart to which the pendulum is attached will provide a force on the pendulum.

F = ρ*L*x''

Which results in a torque:

Tmove = 0.5*ρ*L2*cos(a)*x''


Total

The total torque on the standing rod is given by the sum of these torques. Because T=I*a'' (I = ρ*L3/3), this allows us to write the ultimate governing equation:

a'' = (3/2*g*sin(a) + x''*cos(a))/L

Approach

We will process the camera images to obtain the current angle of the pole. We will use this information in a feedback system to move the cart under the pendulum and stop its motion. Using modern control theory, we will be able to do this in the most optimum way, minimizing undesirable behavior and stabilizing it as quickly as possible. If we can obtain some estimates of the amount of process noise (wind and such) and the amount of measurement noise (how inaccurate our sensors are), we could use Kalman filtering to optimally stabilize it in the presence of this noise.

Sadly enough, many of the papers we have read for the class are completely irrelevant to this robot. It performs no mapping — so it will not use Monte Carlo Localization [Dellaert], nor other Markov-based probabilist navigation models [Simmons], nor DERVISH's relatively simpler model of the world [Nourbakhsh]. Our pendulum-balancing robot will be so simple as to essentially have one mode of behavior — balancing the pendulum — which makes subsumption architecture [Brooks] irrelevant. While Polly [Horswill] accomplished many things, balancing a pendulum was not among them (nor will our robot give tours). Finally, as our robot will not be humanoid, we will be unable to apply the exemplar-based learning approaches seen in [Drumwright].

There is one paper that will benefit us, however. As it did in the last project, [Mouravec]'s trials and tribulations with the Stanford Cart will remind us that, however bad things may get, they could get much worse.

Photo Gallery
Behold, the inanimate carbon aluminum rod!
The hinge we'll attach it to.
It is currently attached by velcro, but will probably end up duct taped...
The testing setup
The camera's view
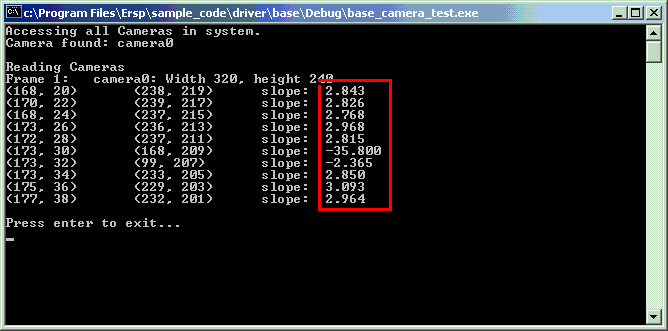
And the result.
Note that most of the slopes were close, while a few were way off. Also, our up and down are reversed, so the slope should be negative.

Bibliography