Example:

Testing whether a graph is acyclic

by Robert M. Keller

What we want to do here are two things:

Get an idea of an informal algorithm for testing graphs.

 

Show how to use our information structure list representations and functions to determine whether a graph is acyclic.

Given some representation of a directed graph, we might like to know whether there are any cycles (loops from a node back to itself, possibly through other nodes).

A graph that has at least one such loop is called cyclic, and one which doesn't is called acyclic. Acylic directed graphs are also called dags.

An acylic graph:

A similar-appearing cylic graph:

Idea:

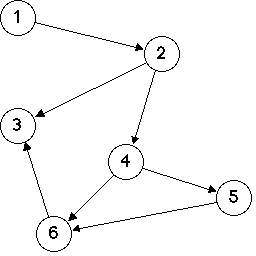
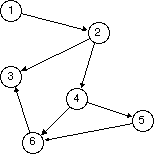
If a graph is acyclic, then it must have at least one node with no targets (called a leaf).

For example, in

node 3 is such a node. There in general may be other nodes, but in this case it is the only one.

This condition (having a leaf) is necessary for the graph to be acyclic, but it isn't sufficient. If it were, the problem would be trivial.

For example, the preceding cyclic graph had a leaf (3):

Continuation of the idea:

If we "peel off" a leaf node in an acyclic graph, then we are always left with an acyclic graph.

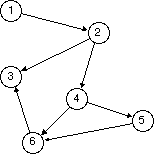
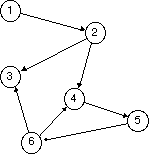
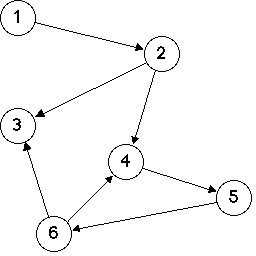
If we keep peeling off leaf nodes, one of two things will happen:

 

We will eventually peel off all nodes: The graph is acyclic.

OR

We will get to a point where there is no leaf, yet the graph is not empty: The graph is cyclic.

An informal statement of the algorithm is as follows:

To test a graph for being acyclic:

1. If the graph has no nodes, stop. The graph is acyclic.

 

2. If the graph has no leaf, stop. The graph is cyclic.

 

3. Choose a leaf of the graph. Remove this leaf and all arcs going into the leaf to get a new graph.

 

4. Go to 1.

The partial correctness of the algorithm is based on the ideas which led to it.

We can see that this algorithm must terminate as follows:

Each time we go from 4 to 1, we do so with a graph which has one fewer node.

Thus, in a number of steps at most equal to the number of nodes in the original graph, the algorithm must terminate.

Partial correctness is a technical term: It means that if the algorithm terminates, it does so with the correct answer.

How can we represent this algorithm in terms of information structures?

Let's choose the list-of-arcs representation for the graph for simplicity.

Recall that for the following graph

the representation would be:

[ [1, 2], [2, 3], [2, 4], [4, 5], [6, 3], [4, 6], [5, 6] ]

First we have to find whether there is a leaf. By definition, a leaf is a node with no arcs leaving it.

The anonymous function

(Pair) => first(Pair) == Node

returns 1 for any Pair having Node as its first element.

The reading of this expression is "the function which, with argument Pair, returns the result of first(Pair) == Node. == is the equality test.

We embed this anonymous function in a call of the rex function find, to give a function is_leaf which will determine whether Node is a leaf:

is_leaf(Node, Graph) =

no((Pair) => first(Pair) == Node, Graph);

Here Graph is our list of arcs. If the call to no returns 1 if, and only if, there is no arc with Node as its first element.

---

Now we have a leaf test. So we next need to use it.

Let's assume that we have a list of the nodes by themselves.

We can test whether any of these is a leaf, and if so, return the identity of the leaf, by:

find_leaf(Graph) =

find((Node) => is_leaf(Node, Graph), nodes(Graph));

If find_leaf returns [ ], there is no leaf. If it returns a non-empty list, then the first element in that list is a leaf.

We can also create one more descriptive function:

no_leaf(Graph) = find_leaf(Graph) == [ ];

How to get the list of nodes:

Think of the list of pairs as a (very bushy) tree.

Example:

For the list

[ [1, 2], [2, 3], [2, 4], [4, 5], [6, 3], [4, 6], [5, 6] ]

the bushy tree is:

The rex function leaves acting on this tree will return a list of all nodes, possibly with duplicates. By applying remove_duplicates to this list, we will get a list of the nodes:

nodes(Graph) =

remove_duplicates(leaves(Graph));

Caution: The "leaves" of this tree aren't only the leaf nodes of the original graph; they include all the nodes, as desired.

Now we are ready to cast the steps of the algorithm in terms of functions.

To start, let Graph be the original graph (as a list of pairs).

1. If the Graph has no nodes, stop. The original graph is acyclic.

We can test this by checking whether Graph is [ ]. If it has no nodes, it has no arcs either, and vice-versa.

2. If the graph has no leaf, stop. The graph is cyclic.

We can test this by computing no_leaf(Graph). If the result is [ ], the graph has no leaf.

3. Choose a leaf of Graph. Remove this leaf and all arcs going into the leaf to get a new graph.

We need one more function: remove_leaf to remove a leaf from a graph.

4. Go to 1.

The spirit of functional programming is that we don't actually remove something from a list; instead we build a new list without the thing to be removed in it.

Suppose Leaf is the leaf to be removed. Then we need only drop all arcs with Leaf as its second element (it will never be a first element; why?):

remove_leaf(Leaf, Graph) =

drop((Pair) => second(Pair) == Leaf, Graph);

As usual,

(Pair) => second(Pair) == Leaf

is an anonymous function which is 1 for a pair with second element being a leaf.

We can simplify this function, provided we only call it knowing there is a leaf:

remove_leaf(Graph) =

remove_leaf(first(find_leaf(Graph)), Graph);

Finally, we need to package the calls to these functions in such a way that iteration is achieved. This is simple, if we use conditional expressions:

The form

P ? T : F

evaluates to the value of T if P is true and to the value of F if P is false.

The overall function for testing acyclicity uses two conditional expressions:

acyclic(Graph) =

Graph == [ ] ? 1 // empty graph is acyclic

: no_leaf(Graph) ? 0 // graph with no leaf is cyclic

: acyclic(remove_leaf(Graph)); // try reduced graph

---

A complete file acyclic.rex with comments and two test cases maybe found as acylic.rex. This may be run in rex by

rex acyclic.rex

Once the file is loaded, you may try any of the examples individually. The two graphs used as examples here are examples graph1 and graph2 in the file.

Disclaimer: We make no statement that this method is the most efficient. Other more efficient ways to achieve the same result are known. This example served to illustrate several functional programming ideas and the progression from an informal algorithm to a working functional program.