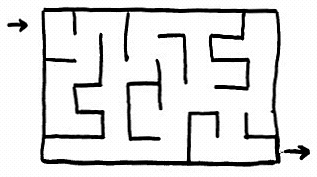
Using a Queue to Solve a Maze

Using a Queue to Solve a Maze (a6)

A maze may be regarded as an implied undirected graph

Two ways to search a graph:

Depth first

Breadth first

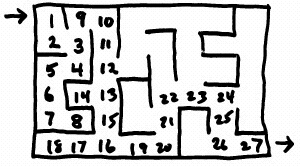
Depth-first order

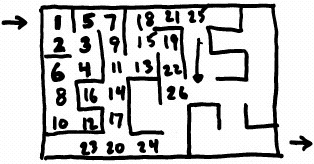
Breadth-First order

Data Abstractions for Searching:

Depth First:

Recursion

or

Stack

Breadth First:

Queue

As an item is removed from the stack or queue, its "unseen" neighbors are inserted.

e.g. breadth-first

suppose 3 is on front of the queue

Its neighbors 4 and 5 are enqueued:

When 4 is dequeued, its neighbor 6 is enqued (3 is already seen)

e.g. depth-first

suppose 3 is on top of stack

Its neighbors 4 and 9 are pushed onto the stack. 2 is not, as it is already "seen".

4's neighbor 5 is then pushed (3 is seen).

Note: The number ordering is not pre-assigned; it is being used for convenience.

Nodes are represented by their coordinates.

The key property of queue, breadth-first:

Items are removed in order of their distance from the starting item.

This ensures that the shortest path is found, if there is a path at all.

The process stops if the queue becomes empty ; this means there is no path.

Knowing when a neighbor is "seen":

Slow way:

Keep a list of seen neighbors.

Fast way:

Keep a bit array, indicating whether each node is seen or not.

When a node is first seen, its bit is set.

Before pushing or enqueuing, check this bit.

For a6, it is advised that you adapt your StringListQueue to a queue of points representing nodes in the graph.

Use class Point from java.awt for example.

Using another array of Point corresponding to each element in the maze, allow each element to point to its "predecessor" in the breadth-first tree.