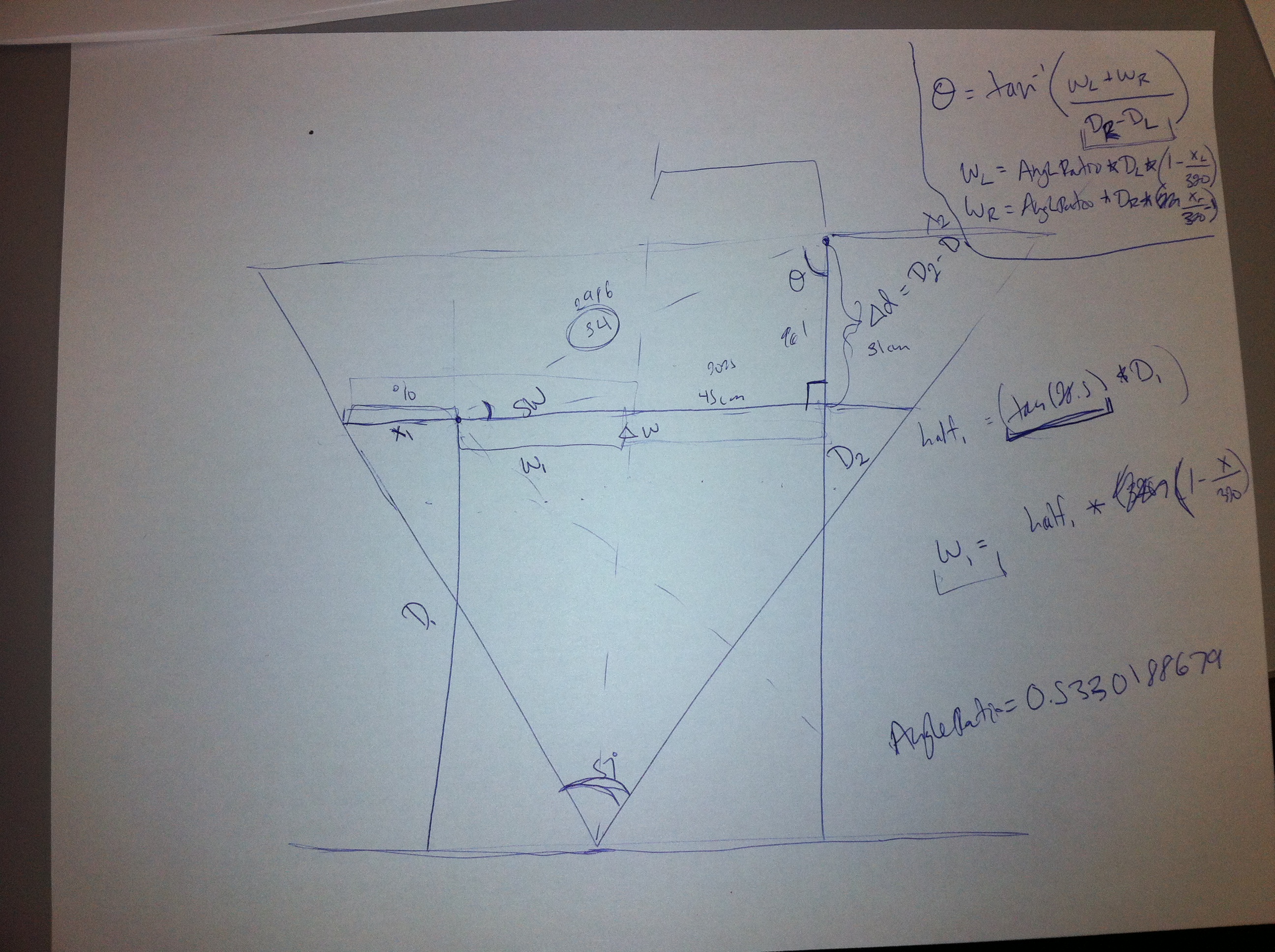
After Prof. Dodds gave us the hint in class, we were able to use some geometry to estimate the angles of walls. Specifically, we did the following:

Essentially, we calculated the distances of the left and right endpoints from the center of the picture in meters and the difference in their distances. This was enough to give us two sides of a right triangle from which we could calculate the angle using the arctangent function.
When we found the left and right endpoints of the box, we were able to use the depth of each endpoint to calculate the width of the camera's field of view at that point. From there, we found the conversion factor between meters and pixels at that depth, and used it to find the physical distance from that point to the center of the image. In the image above, those distances correspond to wl and wr respectively. (Note: in the above image, the value of theta that we calculated is not the correct angle, so we flipped the argument of the arctangent function to find the right one.)
There is a possible slight limitation on our algorithm, however. Since we calculate the distance from the center of the image, if the box is entirely in one half of the image, then we may not be able to calculate the angle of the box correctly. We tried this, and it was fairly difficult to determine whether we were calculating the angle correctly, since by our estimations it would be off by ~10 degrees.
Bonus! We were able to automate this process by finding the endpoints of the box in the following way: starting at the center of the image, we would search left and right one pixel at a time until we found a significant change in depth (or a distance of nan). Then, we could use these as our endpoints and apply the above algorithm to find the distance. (The alternative to this was to manually click and specify the left and right endpoints in the image.) This proved to be quite accurate, although it does only work if the center of the image is part of the box.
Because we worked out the geometry on paper first, we found that the lab went quite smoothly. We had a couple typos that were pretty difficult to debug, since we couldn't tell what the correct answer was supposed to be in some cases. The geometry was relatively straightforward compared to that of the last assignment.
We have a couple suggestions for improvement. First, it might be useful to provide the students with some test cases, perhaps by giving them an image with the box and distance data in it where the angle is known. This would allow the students to determine whether or not their approach was working. (Of course, providing this image and the distance data in such a way that it can be converted to an OpenCV image might be a bit difficult.) We also would suggest that the students have the explanation given in class on the Kinect's field of view and the basic geometry of the problem. Even questions like "What information do you need to calculate the angle, say from a trigonometric perspective?" or something to that effect could be helpful.