The Futility of Bias-Free Learning and Search

2019

Overview

Imagine you are on a routine grocery shopping trip and plan to buy some bananas. You know that the store carries both good and bad bananas which you must search through. There are multiple ways you can go about your search.

You could:
1) randomly pick any ten bananas available on the shelf (unbiased search)
2) Only pick those bananas that are neither unripe nor overripe (biased search)

If your search algorithm is biased in the right ways, you'll perform better. Sampling in the second way will produce a better yield of good bananas. We show that bias powers artificial learning; without properly-aligned biases, learning algorithms perform no better in expectation than uniform random samplers.

We also find that an algorithm cannot be simultaneously biased towards all types of bananas (unripe, overripe, perfect).

Key Definitions

Bias

Statistical bias is when the expected value of a parameter differs from its baseline (true) value.

We define algorithmic bias to be a measure of how different the performance of an algorithm is with respect to a uniform random sampling baseline.

Given a:
• $k$-sized fixed target $t$ (represented as a $k$-hot vector)
• distribution over information resources $\mathcal{D}$
• search strategy $\overline{P}_F$ (i.e., inductive orientation relative to $F$)
• performance of uniform random sampling $p$
$$\text{Bias}(\mathcal{D},t) = \mathbb{E}_{\mathcal{D}}\left[ t^{\top} \overline{P}_F \right] - p$$ Note: algorithmic bias has very little to do with unethical human biases (racial, xenophobic, etc.). Our version of algorithmic bias is strictly defined in the domain of mathematics, and human examples of it include picking the simplest solution from a set, and choosing a particular type of learning algorithm to solve a problem.

Target Divergence

What does algorithmic bias look like? Target divergence is a geometric interpretation of it which measures the angle between the target vector $t$ and the averaged $|\Omega|$-length simplex vector $\overline{P}_f$ using cosine similarity.

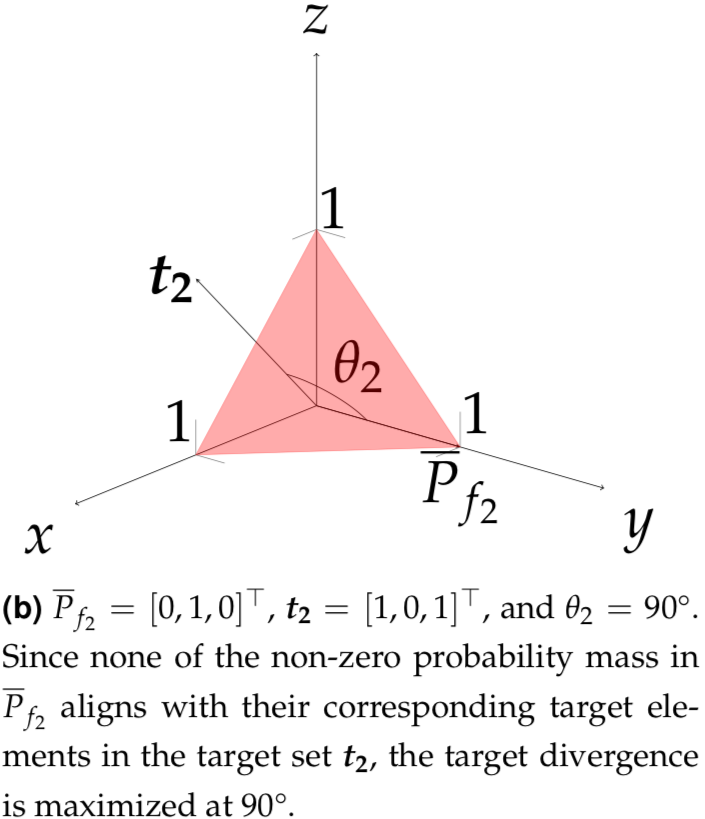
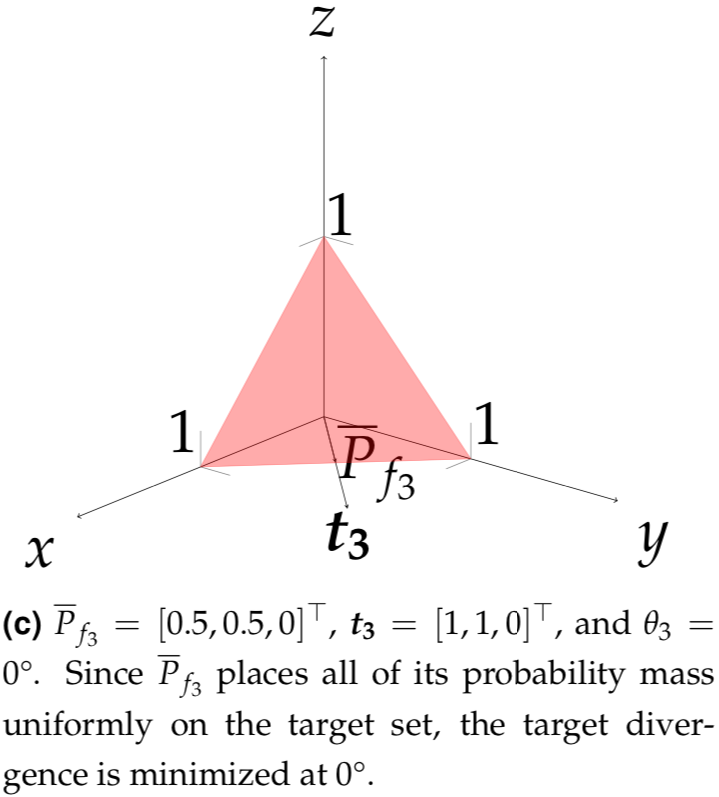
Selected Results

Improbability of Favorable Information Resources

Let $F$ be a random variable such that $F$ ~ $\mathcal{D}$ and let $q(t,F)$ be the expected per-query probability of success for algorithm $\mathcal{A}$ on search problem $(\Omega, t, F)$. Then for any $q_{min}$ $\in$ [0,1], $$\mathbb{P}(q(t,F) \geq q_{min}) \leq \frac{p + \text{Bias}(\mathcal{D}, t)}{q_{min}}.$$ Using the per-query probability of success from The Famine of Forte, we bound the probability that an algorithm is successful, in terms of its bias. This shows that one is unlikely to encounter highly favorable information resources when sampling under $\mathcal{D}$ unless the algorithm is tuned to that particular target $t$.

Conservation of Bias over Distributions

Let $F$ be a random variable such that $F$ ~ $\mathcal{D}$ and let $q(t,F)$ be the expected per-query probability of success for algorithm $\mathcal{A}$ on search problem $(\Omega, t, F)$. Then for any $q_{min}$ $\in$ [0,1], $$\sum_{t \in \tau_{k}} \int_{\mathcal{P}} \text{Bias}(\mathcal{D},t) d\mathcal{D} = 0.$$ Similar to conservation laws for energy and mass in physics, we show that bias is a conserved quantity.

An algorithm can have positive bias on a particular target, but this implies it also has negative bias on some other targets in the search space. We show that the total bias an algorithm has is 0, thus bias encodes trade-offs and we must choose which targets we want to be biased towards.

This further means that an algorithm cannot be biased towards all possible targets such that it would perform well on all problems.

Futility of Bias-Free Search

If $ \text{Bias}(\mathcal{D},t) = 0 $ then, $$ \mathbb{P}(\omega \in t; \mathcal{A}) = p. $$ Our bias quantity essentially captures how much more likely an algorithm is to find an acceptable model to fit some data than by picking a model at random. Thus when an algorithm has no bias, the probability it will find an acceptable model is equal to the probability of it uniformly randomly sampling from a set of possible models.

Additional Resources

[ Paper (PDF) ]

Authors

Jonathan Hayase

Julius Lauw

Dominique Macias

Akshay Trikha

Julia Vendemiatti

George Montañez

Acknowledgements

We'd like to thank our loving families and supportive friends, and the Walter Bradley Center for Natural and Artificial Intelligence for their generous support of this research.