The Hero's Dilemma

2020

Overview

In a bleak and desperate world short on food, medicine and supplies, you lead a group of survivors on a predawn supply run. Unfortunately, you and your companions are not the only survivors searching for food that morning. One of your lookouts spots a band of scavengers from an enemy camp slowly making their way toward your location. You have no reason to believe that they're aware of your presence; with stealth a direct confrontation might be avoided. The enemies are heavily armed, so any confrontation would likely prove fatal. Quickly, you motion for your team to hide and wait. To your dismay, the enemies reach your location and decide to enter. They are set on finding supplies themselves but instead find nothing. Lying in wait, your stomach sickens as you watch their frustrations rise and their suspicions mount that they might not be alone.

You can order your team to remain hidden and risk being discovered, or you can initiate an ambush, which would at least give you the advantage of a surprise attack. If discovered, you would lose your supplies and perhaps your lives, but fighting carries with it an even smaller chance of survival. You signal to prepare an attack, but determine that you will only fire once it becomes clear you have been discovered. Hand poised in the air, trembling but ready to signal, you ask yourself: have I made the right choice?

In this study, we test the outcomes of a simple two-player game in which an agent must decide whether to fight another agent, based on the perceived intentional stance of the other agent. For each altercation there is a chance of death, but there is an advantage to striking first if currently undetected by the adversarial agent. In one scenario, the second agent can perceive that an attack is intended, and in the other scenario, the second agent cannot perceive the intention of the first agent. For non-perceptive agents, we test a variety of strategies such as attacking at random, attacking only in retaliation, and always attacking. For the perceptive agents, the employed strategy is to attack once the adversarial agent has detected them and intends to attack, forfeiting the advantage of surprise but nevertheless striking first. Similar to simulation studies of the famous Prisoner's Dilemma, we use our simulated agent experiments to analyze statistical outcomes, measuring differences in survival rates for various strategies and parameter settings.

Simulation Details

The interactions between hero and adversary are modeled after a first-person dungeon crawl video game, where discrete time steps are used to trigger the two agents' actions. All hero and adversary encounters last a total of ten time steps, where at any given time step each agent is either idle, in its attack cycle, or dead. The attack cycle length \(C\) is the number of time steps between attacks for both hero and adversary agents. That is, after an agent's first attack, the agent will attack every \(C\) time steps until either an agent is killed or ten time steps elapse.

In this project, we compare the following strategies for the hero agent:

NEVER: The hero never enters it's attack cycle.
ALWAYS: The hero enters it's attack cycle on the first time step.
RANDOM: Each time step the hero has a \(P_r\) chance to enter it's attack cycle.
RETALIATE: The hero enters it's cycle after the adversary attacks.
INTENTION: The hero enters it's attack cycle after the adversary enters theirs.
CAUTIOUS: Each time step the hero has a \(P_I\) chance to enter it's attack cycle, where \(P_I\) is computed based on the INTENTION strategy. This is to show that the results of the INTENTION strategy are from the knowledge and not simply an increase or decrease in attack likelihood.

Beginning the encounter, the adversary has a chance \(P_d\) to discover the hero on each time step. If the adversary discovers the hero, it starts its attack cycle which lasts \(C\) time steps. The adversary then strikes at the end of its cycle with a \(P_{k,a}\) chance of killing the hero and starts its next attack cycle. If the hero decides to attack, it begins its attack cycle, of same length \(C\), but attacks at the beginning of its cycle and has a \(P_{k,h}\) chance of killing the adversary. Since the adversary strikes at the end of its cycle while the hero strikes at the start, most cycle values leave a window in which a hero employing the INTENTION strategy can attack after having been detected. However, if the hero has not yet been detected, the probability of the hero killing the adversary on a given attack is \(P_{k,h} + P_{k, s}\) instead of \(P_{k,h}\), where \(P_{k, s}\) represents a boost due to the element of surprise.

We compare the given hero strategies by varying over the parameters listed above.

The code for this project can be found here.

INTENTION

ALWAYS

RETALIATE

Results

INTENTION Strategy Results in Higher Survival Rate in Most Cases

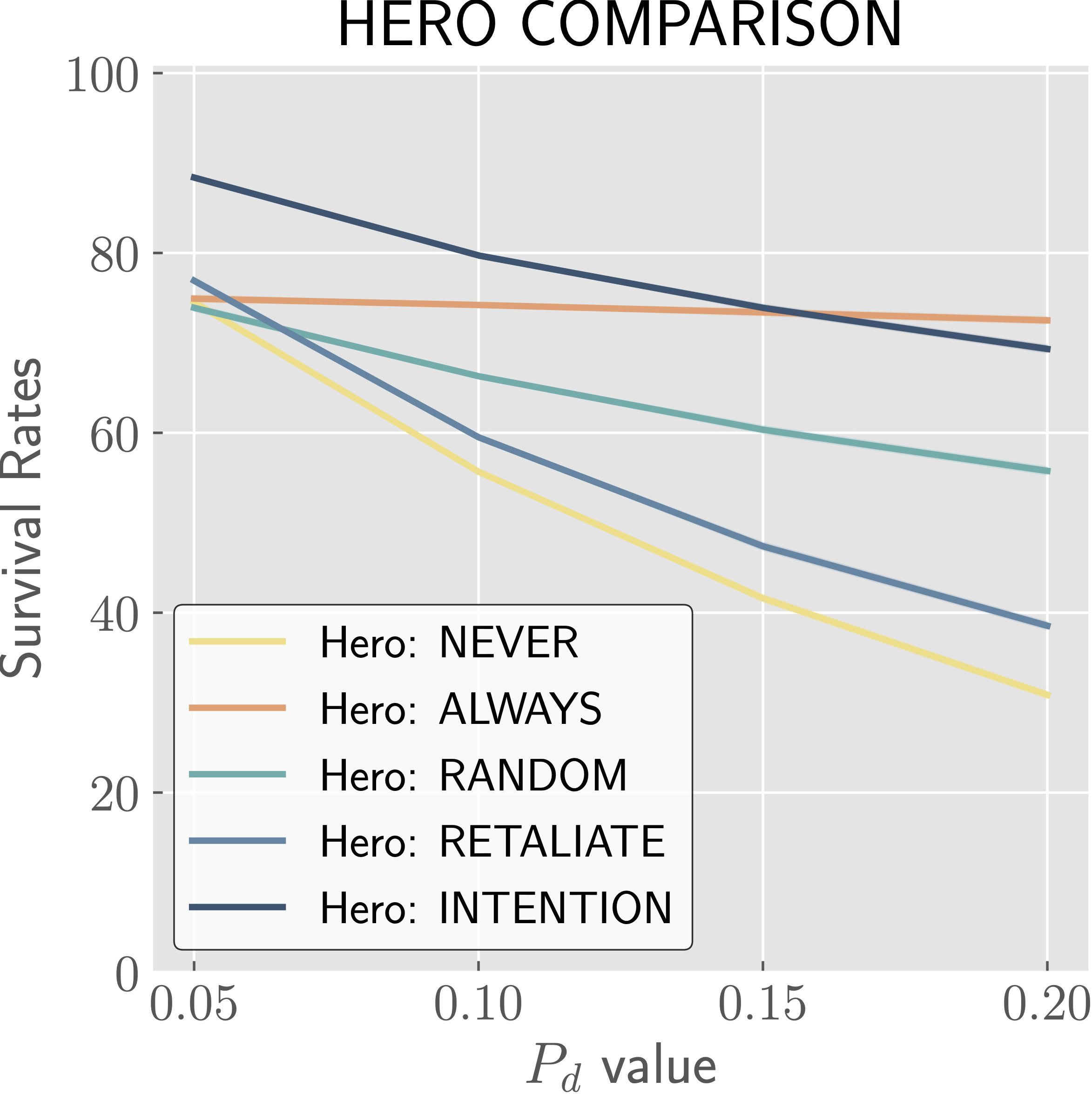
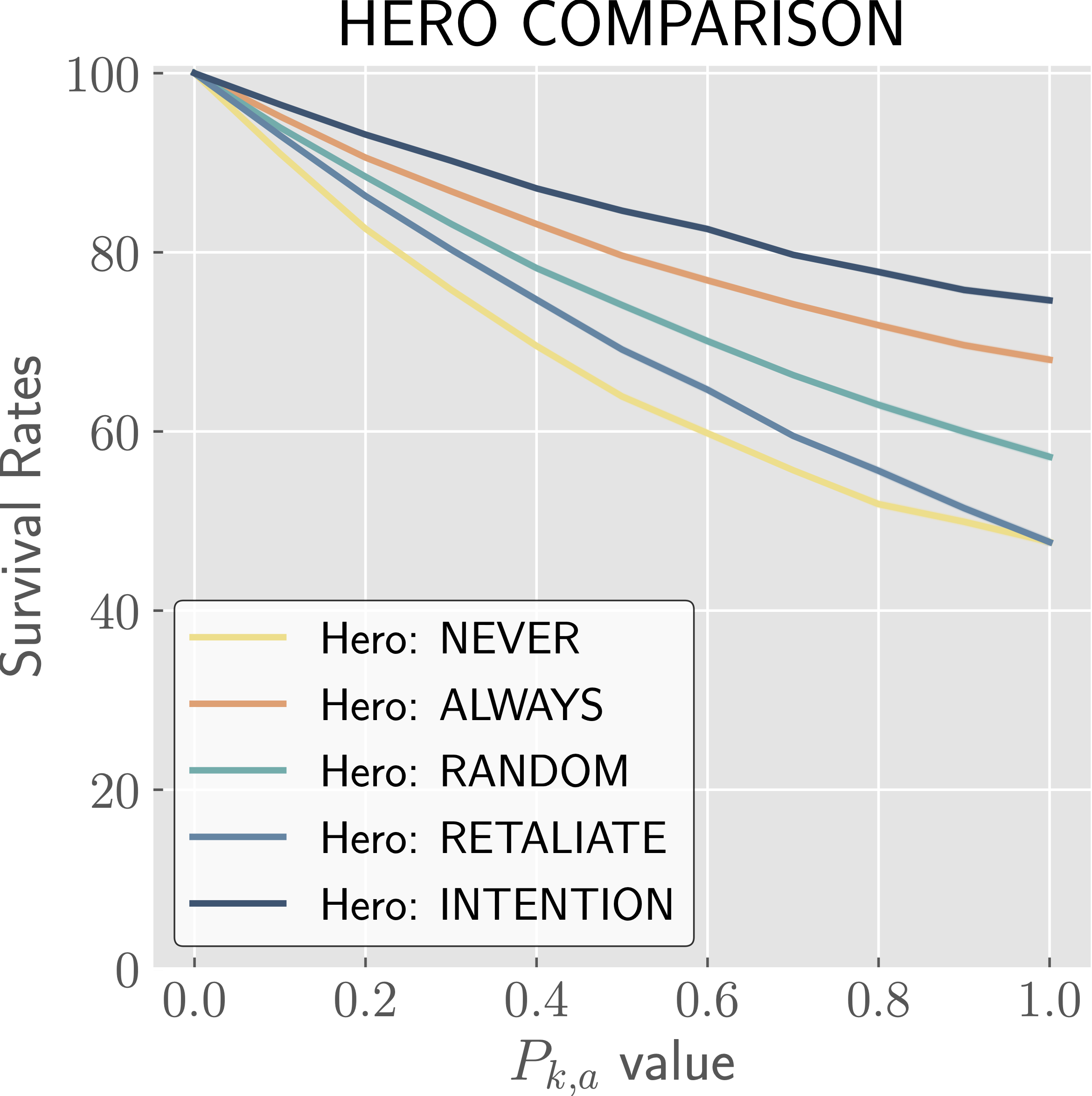
Probability of Kill for Adversary Comparison

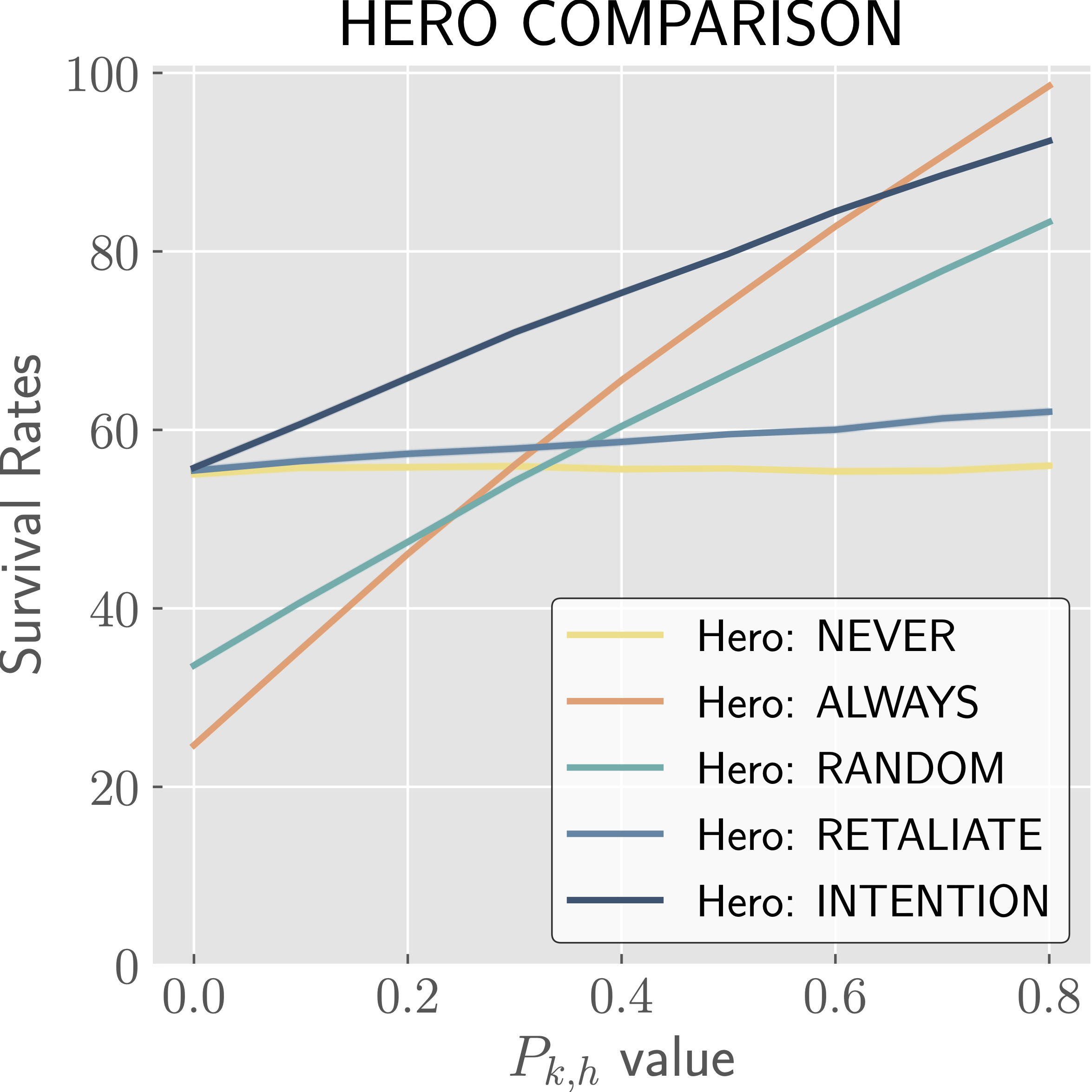
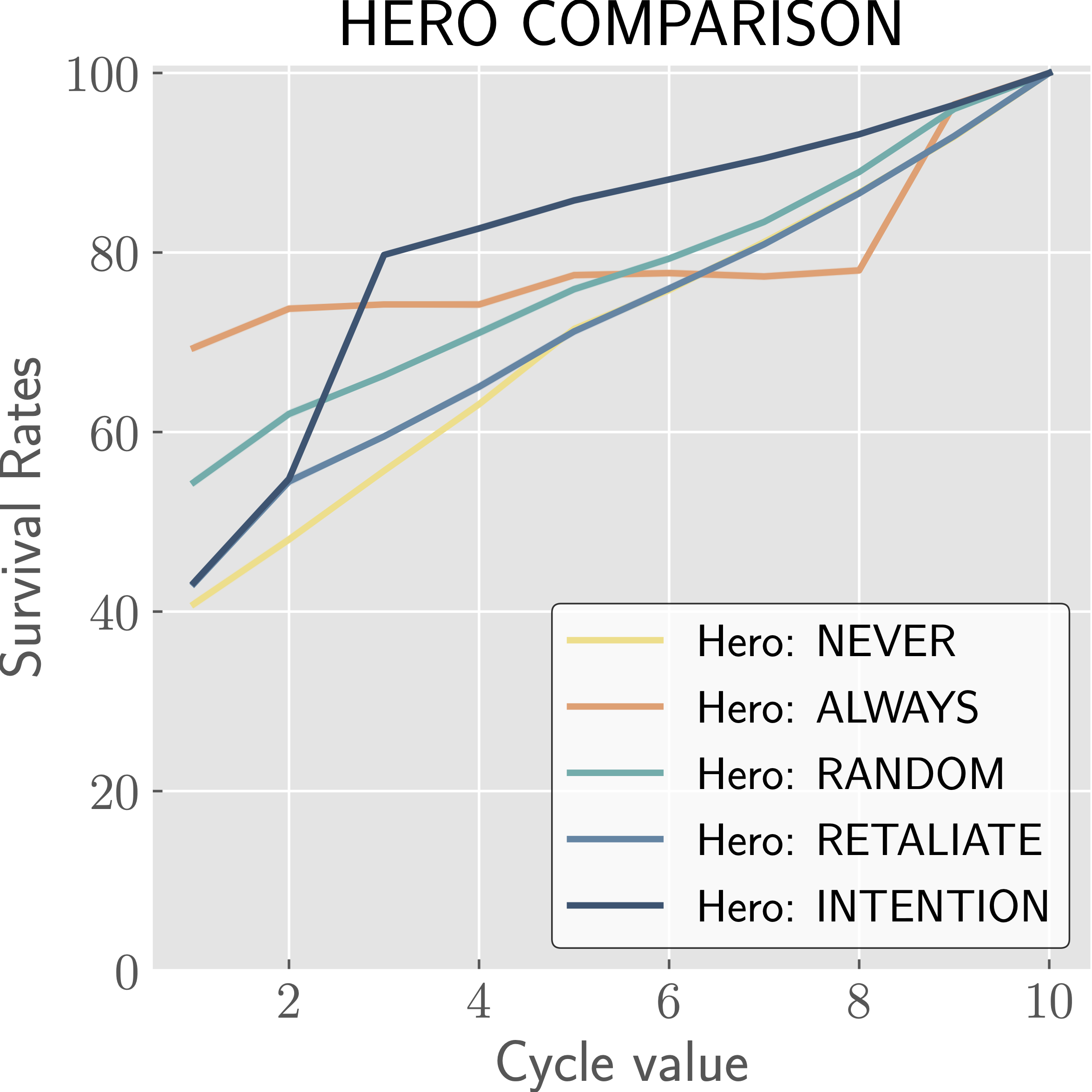
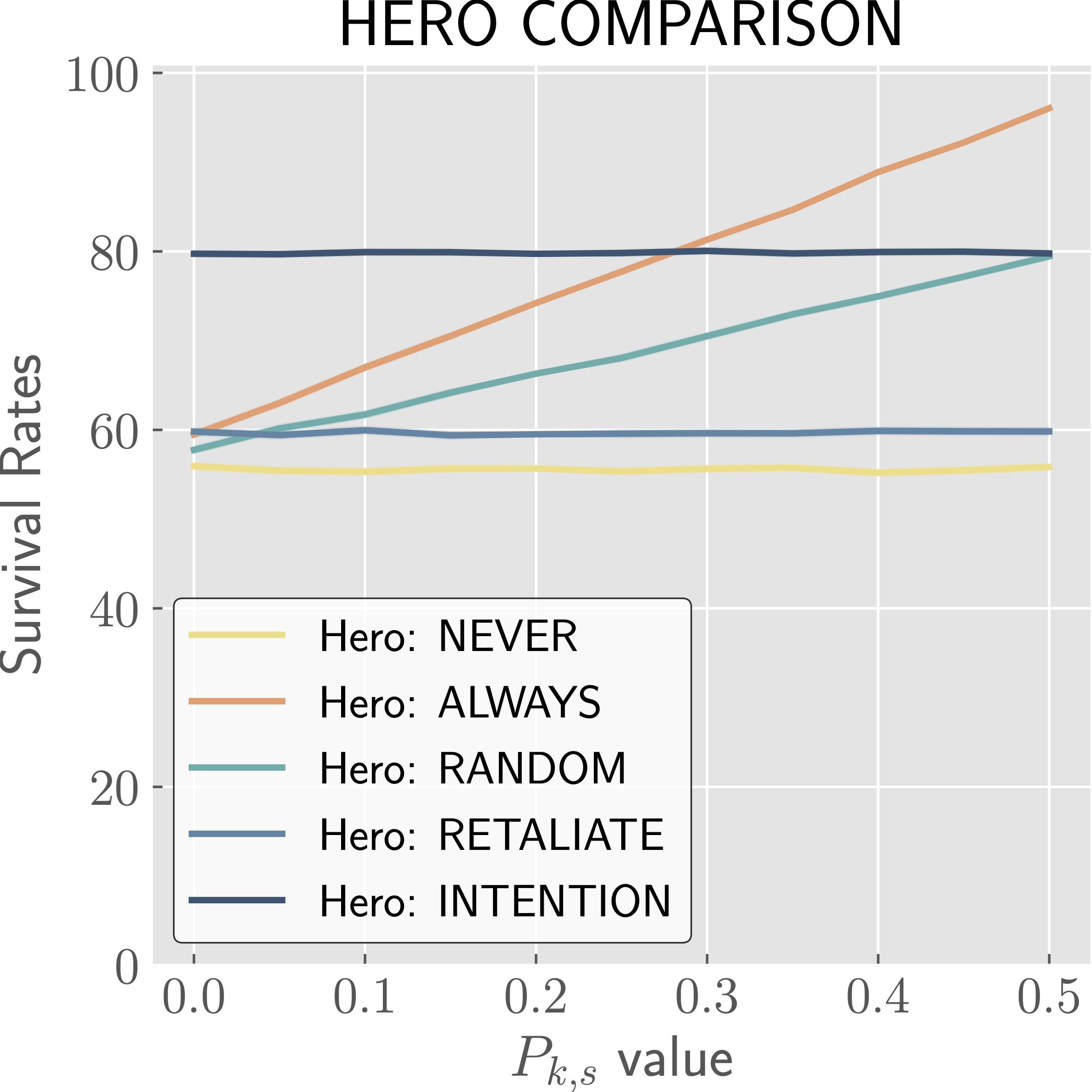
Probability of Kill Boost for Surprise Attack Comparison

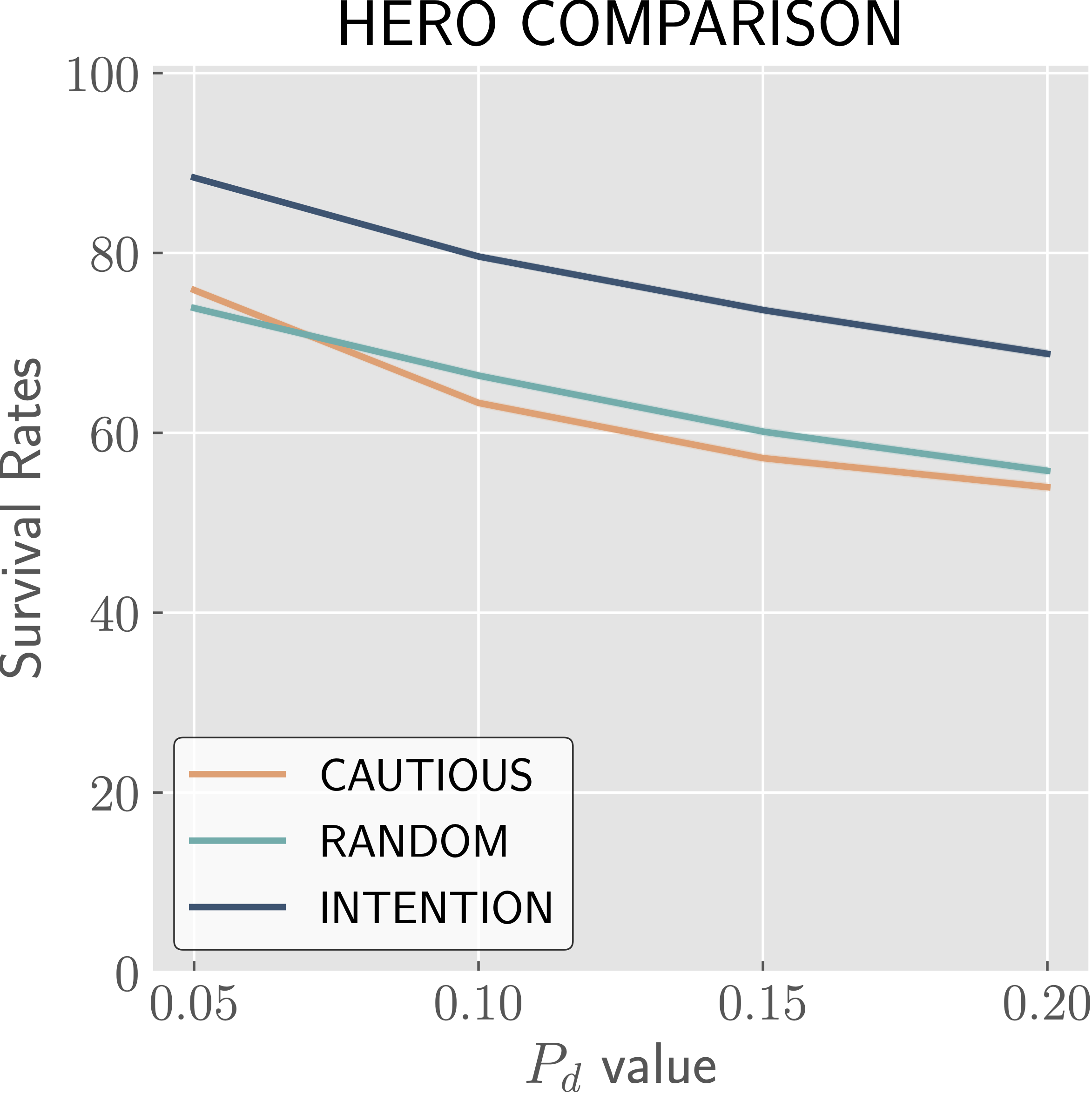
The effects of varying different parameters on HERO survival rates in regards to indicated strategies.

We see that in most cases, the INTENTION strategy performs the best with respect to hero survival, with the ALWAYS strategy occasionally surpassing it. These cases are fairly intuitive. When being detected is almost certain, it is best to attack. When you have a high chance of killing the adversary, from base \(P_{k,h}\) or with boost \(P_{k,s}\), there is no reason not to attack (unless you care about adversary survival as well, in which case INTENTION provides a good balance—see the paper for more details). We also see that when the cycle is too short to leave a window open for the INTENTION strategy, it performs equivalently to RETALIATE and thus worse than ALWAYS. Lastly, we note that the CAUTIOUS strategy generally performs worse than RANDOM, and significantly worse than INTENTION, and so we know that the INTENTION strategy excels due to the knowledge of when to attack rather than an increased or decreased likelihood to attack.

Attacking First is Important

Probability of Kill Versus Cycle Heat Map

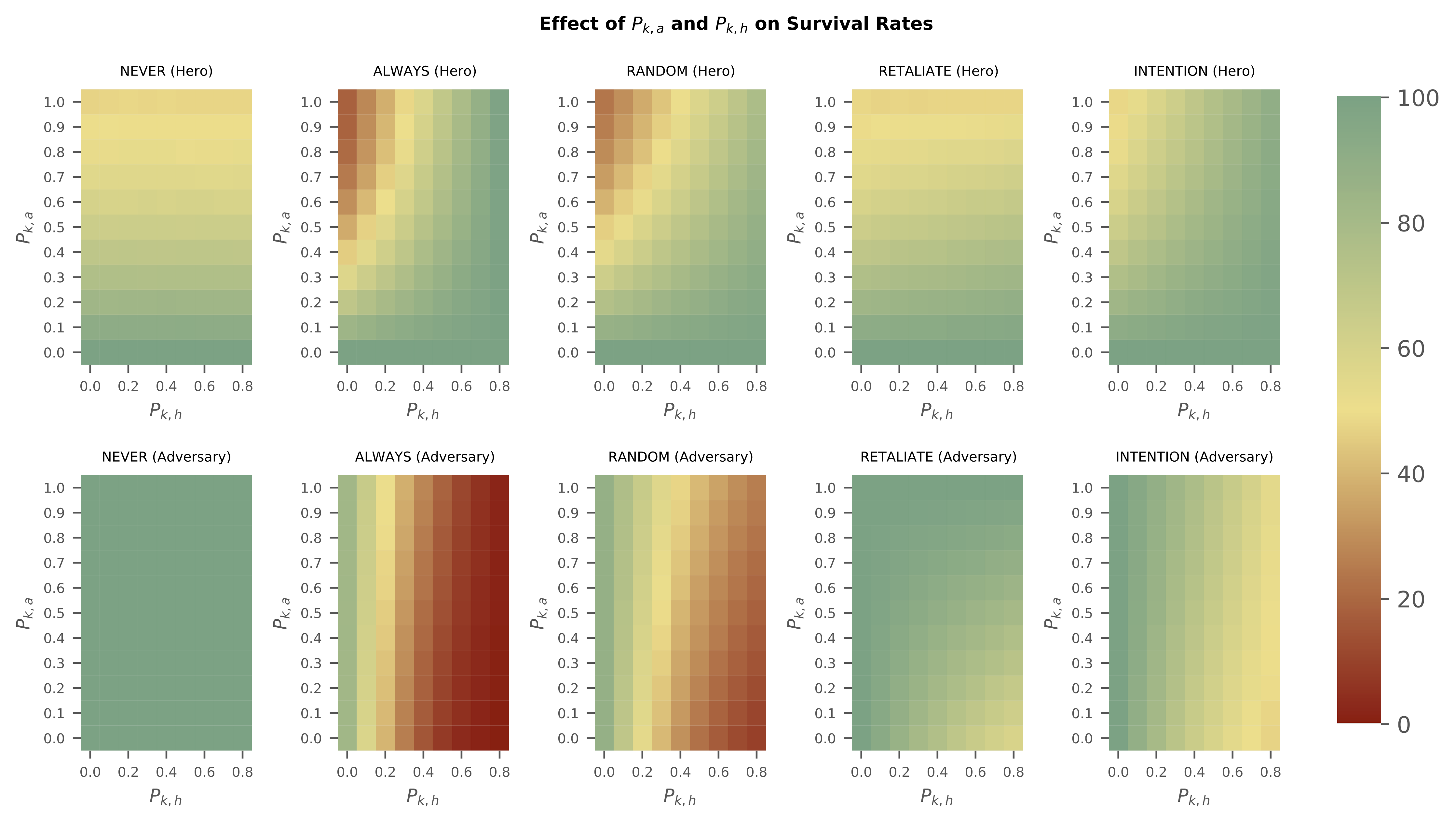
Our main observation in the first heat map is that if an agent is attacked first, their survival depends most strongly on the opponent's attack strength. For NEVER and RETALIATE, we see primarily a vertical gradient for the hero, showing that survival depends on the adversary's probability of killing the hero. For ALWAYS, RANDOM, and INTENTION, strategies which usually attack first, we see primarily a horizontal gradient for the adversary, indicating that their survival depends on the hero's probability of killing the adversary. These trends are not replicated in the agent that attacks first, as we see a fairly diagonal gradient for hero's using ALWAYS, RANDOM, and INTENTION.

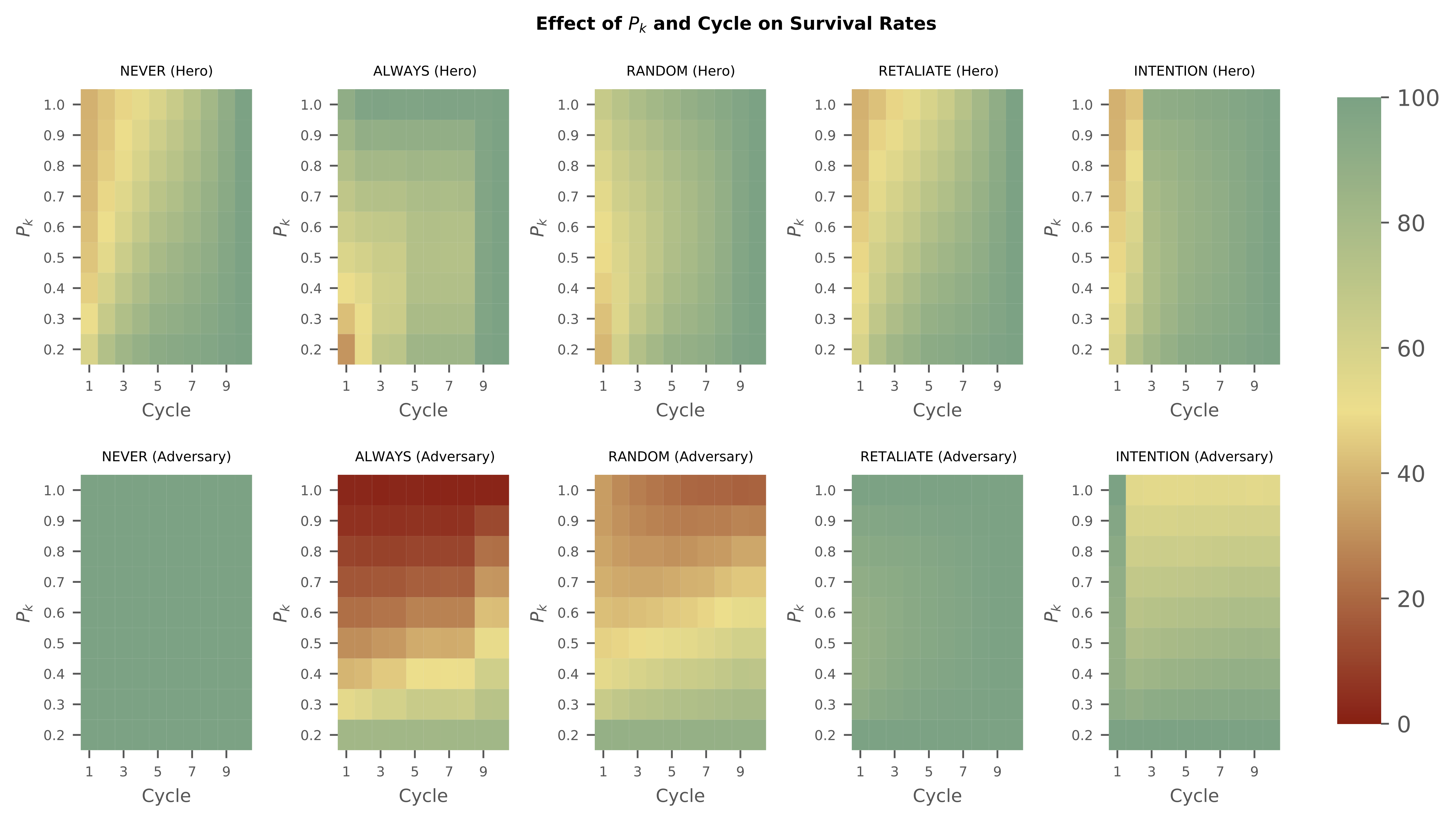
In the second heat map, we varied \(P_{k, h}\) and \(P_{k,a}\) together, calling it \(P_k\), and see that defensive strategies (INTENTION, RETALIATE, NEVER) fare worse at high \(P_k\), and that offensive strategies (ALWAYS, RANDOM) fare worse with low \(P_k\) values. We also note that all strategies performed better at larger cycle values, since the adversary becomes less likely to complete their attack.

Overall, we find that agents using the INTENTION strategy have the highest survival rate in almost all cases—when (a) the hero's first attack is weaker than the adversary's, (b) when it is possible to detect the adversary's intentions and strike before being struck, and (c) when it is relatively unlikely for the adversary to discover the hero. In general, the best strategy in this type of situation depends primarily upon the agents' probability of being detected and relative strength to their opponent. Not only does INTENTION enable the hero agent to have the best survival rate, but it is also the best strategy to minimize overall damage. By limiting unnecessary attacks on both the adversary and the hero, an INTENTION strategy could be seen as an important component of strong, yet cooperative, diplomacy. These results provide evidence of the usefulness of intention perception in agents. Having a model of the minds of other agents, being able to attribute intentions to them and act accordingly, would seem to be as useful in virtual worlds as it is in our own.

Additional Resources

[ Paper (PDF) | Presentation | Code ]

Authors

Amani Maina-Kilaas

George Montañez

Cynthia Hom

Kevin Ginta

Cindy Lay

Acknowledgements

Special thanks to Jerry Liang, Aditya Khant, Kyle Rong, and Tim Buchheim for assistance in experimental set-up. This research was supported in part by the National Science Foundation under Grant No. 1950885. Any opinions, findings or conclusions expressed are the authors' alone, and do not necessarily reflect the views of the National Science Foundation.