What Makes Neural Architecture Search Work?

2023

Overview

You've probably heard some of the buzz around machine learning and its amazing capabilities, such as classifying images, having fluent conversations with humans, or beating humans at some of the hardest known board games. Maybe you have even considered designing your own novel model. However, it is challenging for someone to get started with building a model if they don't already know a lot about machine learning. You would need to spend an enormous amount of time learning theory and code to create a useful model catered to your problem. What if you didn't need to be an expert at machine learning? What if you could have a computer itself do the work for you? Imagine if a computer could find an optimal machine learning model for your problem with minimal human intervention! That is where neural architecture search (NAS) comes into play.

Because neural architecture search is a newer field, you still need a deeper understanding of machine learning to implement such techniques. There are so many algorithms to choose from (reinforcement learning, genetic algorithms, neuroevolution, and differentiable relaxation, to name a few) and no established guidelines on how to choose an approach. Our project aims to shed light on how these methods are working on a fundamental level so that the process of generating better architectures with each generation is easy and intuitive. We aim to do this by analyzing the locality of the neural architecture search space as well as the effect of search method on improvement during the search process. Hopefully our work can lead to a unifying framework for NAS.

Key Definitions

Neural Architecture (aka Neural Network)

A neural architecture is a model that yields output from input data (e.g., feeding an image to a neural network outputs a classification). A neural architecture can be visualized as a directed acylic graph, where the input data is taken through intermediary calculations to produce the final output. We can break up the input data into nodes. These nodes collectively represent the input layer. This input layer flows through the hidden layers (i.e., intermediary calculations) to eventually produce output.

Hyperparameters and Parameters: Hyperparameters are the independent variables that can be manually adjusted for the training process of a neural architectures. Parameters are the variables that the neural architecture training algorithm discovers. The usual goal of a machine learning problem is to find the right set of hyperparameters and parameters to solve a task.

Multilayer Perceptron (MLP) (aka Fully Connected Layer): The first type of neural network to be developed. Every other type of neural network either draws inspiration from an MLP or has it as a component. The connection arrows represent weights, which are multiplicative mappings from one layer to the next.

Credit: https://commons.m.wikimedia.org/wiki/File:MultiLayerNeuralNetworkBigger_english.png

Convolutional Neural Network (CNN): This type of model specializes in image classification. A CNN attempts through to learn features and structures of an image (e.g., the shapes of human ears and eyes) through convolutions, which are another kind of multiplicative mapping. These convolutions normally shrink down the input/intermediary image being processed. Neural architecture search research typically focuses on CNNs. A multilayer perceptron usually comes at the end of a CNN to eventually yield final output.

Credit: https://commons.wikimedia.org/wiki/File:Typical_cnn.png

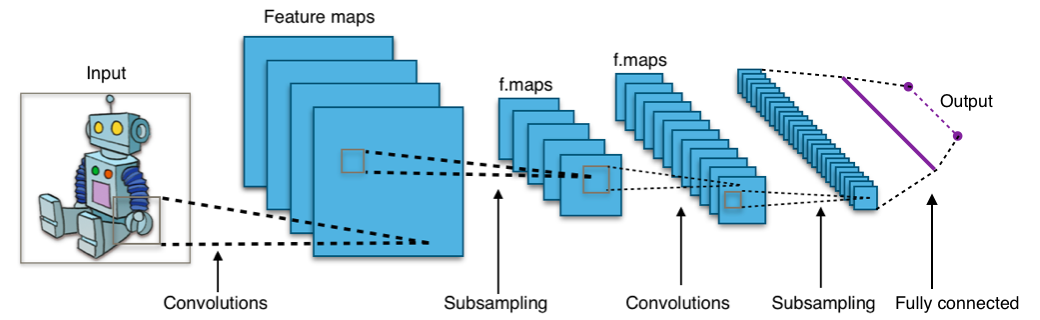
Neural Architecture Search (NAS)

A joint optimization problem where both the optimal neural architectures and the associated hyperparameters/parameters need to be found. Usually, the process of finding the hyperparameters/parameters is fixed, and NAS just focuses on the higher-level search. You can think of NAS as searching for a good topology of a neural architecture for a given problem.

Search Space: Constraints on the types of neural architectures that may be produced. Typically, these constraints make the architectures found similar, in principle, to well-known, manually-designed architectures. Check out this example.

Search Method: The algorithm that explores the search space (e.g., reinforcement learning or genetic algorithms).

Performance Estimation Strategy: It is potentially computationally expensive to train a single architectures, let alone hundreds or thousands of them, to find the architectures with optimal metric values (for example, the highest validation accuracy in a certain dataset). Therefore, performance estimation strategies are essentially heruistics to approximate these metrics, to save computational resources and time.

The Problem of Reproducibility

When NAS was first emerging, there were two major challenges that made research difficult to reproduce. First, NAS algorithms were very expensive. For example, Zoph & Le's first method using reinforcement learning used 800 GPUs! This expensive cost made NAS research virtually inaccessible to researchers without these resources. Secondly, many algorithms used their own search spaces so there wasn't a fair benchmark to compare algorithms against.

NAS Benchmarks

Enter... NAS Benchmarks. In 2019, Ying et al. created NAS-Bench-101, which addressed both of these problems. NAS-Bench-101 consisted of training data from 423k architectures in a tabular format. This meant that computation would not be such a huge barrier to entry anymore, because researchers could simply query the training result in NAS-Bench-101 rather than having to train the architectures themselves. Next, NAS-Bench-101 also provided a point of comparison for different algorithms. NAS-Bench-101 later led to the development of a whole suite of NAS Benchmarks, including NATS-Bench, which is the one we use.

NATS-Bench

NATS-Bench consists of two search spaces, a search space on size and a search space on topology, which is the one we are interested in. Architectures in this search space consist of stacks of cells, with each cell having 4 nodes, 6 edges, and 5 types of edges for a total of 15,625 possible architectures. Each architecture has training data for imagesets CIFAR-10, CIFAR-100, and ImageNet16

NAS as a Graph

We can abstract any given search process into a graph on the space of neural architectures. The edge going from architecture A to architecture B indicates the probability that architecture B will be selected in the next iteration, given architecture A as the previous architecture. (This, of course, assumes a Markov structure on the search process. This limitation can be eased for transformations that make use of bounded historical information by embedding such information in the nodes themselves.) An edge of weight 0 is equivalent to having no edge between architectures. Each iteration, the search method bounces from architecture to architecture, using these assigned weights.

Definitions

transformation operator: the set of rules that defines the weights of edges on the graph.

neighborhood of an architecture: the set of architectures that are one edge away from the original architecture.

neighbor of an architecture: an architecture belonging to the neighborhood of the original architecture.

graph distance: the path length from one architecture to another, in expectation.

reach: the expected edit distance from one architecture to the next.

improvability: change in score (in our case, accuracy) per iteration.

Experiments

What is the relationship between the average reach of a transformation operator and the improvability of a neural architecture search space? We hypothesize the following:

Transformation operators with larger average reach will:

Have lower improvability than smaller average reach transformation operators on the top 10% architectures
Have higher improvability than smaller reach transformation operators on the worst 10% of architectures
Overall have lower improvability than smaller reach transformation operators if the distribution of architecture accuracies is skewed right (i.e., many accurate architectures)

We aim to falsify or support these hypotheses by generating a large number of transformation operators, which we will then evaluate on the search space. We will run two types of experiments: one where we fix the path length and compare the final and initial scores, and one where we fix a score threshold and record how long it takes to reach that score. Once we have the data, we will calculate Kendall's Tau rank correlation to determine if improvability and reach are correlated.

Authors

Joseph Lee

Marina Ring

George Montañez

D. Tao

Dan Fonseca

Acknowledgements

Special thanks to Kelly Hamamoto, who helped with early iterations of this work, and the entire AMISTAD Lab. This research was supported in part by the National Science Foundation under Grant No. 1950885. Any opinions, findings, or conclusions are those of the authors alone, and do not necessarily reflect the views of the National Science Foundation.