Probabilistic Abduction

2021

Overview

When we make decisions, we often use one of three types of logical inference: deduction, induction, or abduction. Deduction and induction are the two most-studied methods of inference, with abduction introduced and coined by C.S. Peirce (“purse”) in his work on the logic of the scientific method.

We can distinguish abduction, in contrast to deduction and induction, in terms of Peirce‘s example of a bag containing white beans:

1. Deduction:
• Rule: All beans in the bag are white.
• Case: The beans in my hand are from the bag.
• Result: The beans in my hand are white.
2. Induction:
• Case: The beans in my hand are from the bag.
• Result: The beans in my hand are white.
• Rule: All beans in the bag are white.
3. Abduction:
• Result: The beans in my hand are white.
• Rule: All beans in the bag are white.
• Case: The beans in my hand are from the bag.

As shown below, we can represent deduction, induction, and abduction using the language of probabilistic machine learning, where labels correspond to the case, generation corresponds to the rule, and data correspond to the result.

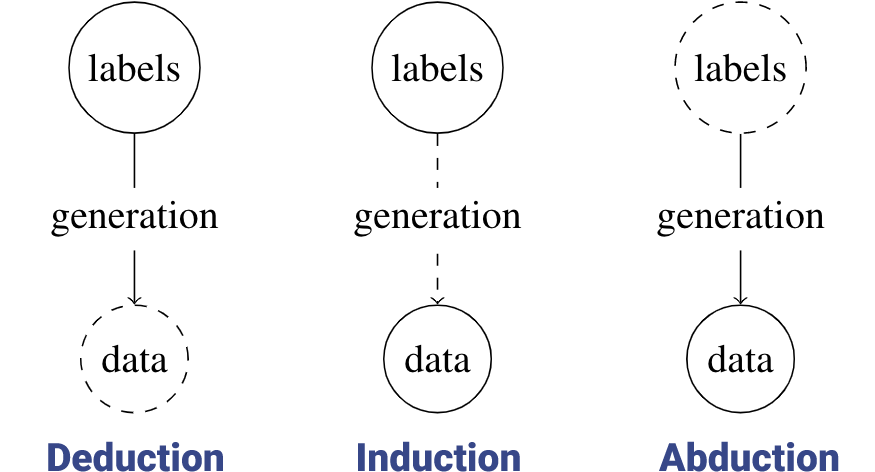
In modern literature, abduction is characterized as a method of finding hypotheses that explain a set of (often incomplete) observed effects or results. In this work, we present a formalization for abductive reasoning by framing abduction in terms of probabilistic, machine learning, and information-theoretic concepts. While abduction has been broadly studied in the field of philosophy and is widely used in human reasoning, its use has not been fully justified. Therefore, we provide preliminary justifications for abduction by mapping key elements in abduction to their corresponding elements in probability, machine learning, and information theory.

Key Symbols and Definitions

• \( \mathcal{X} \): the space of feature vectors (i.e., observed effects represented as vectors)
• \( \mathcal{Y} \): the space of possible labels
• \( x \): a possible feature vector found in \( \mathcal{X} \) that takes the form \(x = [x_1, \ldots, x_n]\), where \( x_i = 1 \) if the feature is present and \(0\) otherwise.
• \( y \): a possible label found in \( \mathcal{Y} \)

Abduction and Machine Learning

We examined the fundamental role of abduction in the inference phase of machine learning. Compare the following schemata for machine learning and logical inference:

Logical Inference	Machine Learning
Induction: \(P(a)\) \(\therefore \forall xP(x)\)	Training: \((x^1,y_1),...,(x^n,y_n)\) \(\therefore f : \mathcal{X} \rightarrow \mathcal{Y}\)
Abduction: \( Q(a) \) \( P(x) \rightarrow Q(x) \) \( \therefore P(a) \)	Classification: \( \mathbf{x}^m \) \( f(\mathbf{x}^m) = y_m \) \( \therefore (\mathbf{x}^m,y_m) \)

The role of induction in the training phase has been studied extensively, but less so for the role of abduction. We propose that abduction is a central tool in the inference phase of machine learning. The unlabelled feature vector constitutes the unexplained predicate \( Q(a) \), and the backwards inference via the induced function \(f\) to arrive at a label is a form of abductive inference. This connection is largely unrecognized, and one of the goals of our project is to bring to light this widespread use of abduction in common machine learning applications.

Tools of Abduction

When we define abduction in terms of probability and machine learning, we use certain intellectual tools to help us find the “best explanation.” We present two integral tools used in machine learning and science: (1) MAP estimation and (2) Occam’s razor.

MAP Explanations

When viewed through a probabilistic lens, we can characterize abduction as finding the explanation that, given the prior probabilities of the observed effects, has the maximal posterior probability. We reduce this instance of abduction to a problem of maximum a posteriori (MAP) estimation. MAP estimation relies on the assumption that the observed effects need to be explained by a single explanation, which elicits a few questions — How can we be sure that the effects are not unrelated, and their coincidental co-occurrence simply due to random chance? What if there are multiple explanations that fit the effects?

To answer these questions, we apply the Famine of Favorable Strategies theorem of Montañez. We find that strongly favorable explanations are rare, and they become more rare as either the threshold for acceptable labels increases or the size of the target set of “close-enough” feature vectors decreases. This alleviates the worry of accidentally finding a plethora of equally good explanations, and suggests that a known explanation class is unlikely to coincidentally raise the probability of many observed features simultaneously, that is, if they are truly unrelated to each other and independent of the explanation under consideration. In other words, if a known entity explains most (or all) of the observed phenomena well, then it probably does not do so by mere coincidence.

Occam’s Razor

In the field of philosophy, Occam’s razor, also known as the law of parsimony, states that the best hypothesis among a set of possible hypotheses is the one that requires the fewest assumptions or entities. When choosing between possible explanations for a set of observed effects, abduction typically yields the most parsimonious explanation as the most likely, thus applying Occam’s razor.

Although Occam’s razor is widely used in abduction, it remains a largely heuristic device that does not have a concrete justification. We provide justification for why Occam’s razor works by relating it to the concept of overfitting in machine learning: using Occam’s razor is analogous to preventing an abductive algorithm from overfitting (i.e., simply memorizing) the observed data. Here we present a few more definitions:

• Generalization error bound (\(P_G\)): Define a generalization error bound of an algorithm \( \mathcal{A} \), trained on the data set \(D\), that outputs a model \(E\) as: $$P_G = \Pr(|R_\mathcal{D}(E) - \hat{R}_D(E)| \leq \epsilon) \geq 1 - \delta, $$ where \(\epsilon\) is an error bound and \((1 - \delta) \in [0, \frac{1}{2})\) is the probability that the true risk \(R_\mathcal{D}(E)\) is not greater than \(\epsilon\) from the empirical risk \(\hat{R}_D(E)\). In English, this is a guarantee that your testing performance won't differ greatly from your training performance.
• Capacity: The capacity of an algorithm \(\mathcal{A}\) is the upper bound on the amount of data that the algorithm can extract from a data set.
• Overfitting (risk relative): An algorithm overfits on a dataset \(D\) when the true risk is greater than the empirical risk.
• Overfitting (information theory): An algorithm overfits on a dataset \(D\) when its output model extracts more data than needed to map every feature vector in \(D\) to its corresponding label.

Thus, we can see that algorithms with greater capacities tend to overfit since they extract too much information from the data set. From these definitions, we note that using Occam’s razor in human abductive reasoning is akin to introducing bias in a machine learning algorithm — namely, biasing \(\mathcal{A}\) to favor simpler explanations through regularization. Thus, we arrive at a justification for Occam’s razor in terms of machine learning:

1. Regularization lowers the effective capacity of the algorithm.
2. Algorithms with lower capacities will not overfit, which in turn reduces the generalization error bound.
3. An algorithm with a lower generalization error bound tends to output models that are more generalizable, which subsequently means its prediction accuracy on future (unknown) data will not deviate significantly from its current observed accuracy.

Hypothesis Generation

When we first come across a surprising instance (i.e., observed effect), we must develop a hypothesis for this instance through abductive inference, a process called hypothesis generation. We characterize hypotheses as being one of two types: inference to the best available explanation (IBAE) and inference to the best explanation (IBE).

We can see that IBE is a special case of IBAE. Most machine learning algorithms operate by outputting an IBAE; for example, in the case of supervised learning, the model can only output a label from a finite set. Thus, the model outputs the label that, based on its training, has the highest probability of explaining the inputted feature vector. However, this output label might not be the best label (i.e., not IBE). This is when we delve into the generation of novel hypotheses.

First, we introduce a corollary to Reichenbach's Common Cause Principle (CCP): If two events are positively correlated but neither is a cause of the other, then there exists a third cause, called the common cause, that these two events are effects of. We can apply CCP to the generation of novel hypotheses.

If the labels \(y_1, \ldots, y_m \in \mathcal{Y}\) are positively pairwise correlated, then we can establish probability flow between these labels and a common cause, \(y_k\). If \(y_k\) raises the conditional probabilities of the existing labels dependent on \(y_k\), then we see that \(y_k\) explains the correlation between the lower-level causes \(y_1, \ldots, y_m\). Thus, \(y_k\) satisfies the explanatory nature of abduction and the unificatory nature of a “good” explanation by Occam's razor.

To our knowledge, there does not exist any well-known machine learning algorithm that can generate a novel hypothesis (i.e., label) based on inputted feature-label pairs. As such, we view our work as a preliminary exploration of human abductive reasoning mapped to core concepts in machine learning, with our confidence in abductive explanations justified by parallels to machine learning.

Authors