Scalability of the Simulation
The nature of an ant colony makes it a very scalable solution to the shortest path problem. Thus, as the number of ants increases, one would expect the average time it takes the ant colony to converge on a shortest path will decrease. To verify this property of the ant simulation, 25 simulations measuring time to path convergence were run and averaged for each of 7 different ant colony sizes both with and without blockages present. The results are plotted on the following graph:
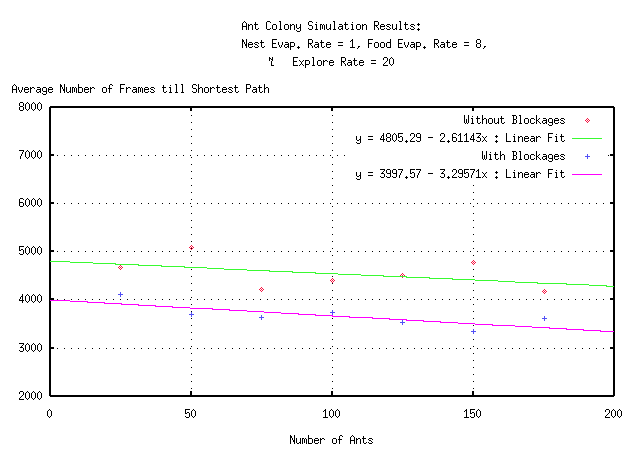
From this graph, it is clear that there is a linear relationship between number of ants in the colony and the convergence time to the shortest path. For every one ant that is added to the colony, the ant colony converges on a shortest path solution about 3 time steps faster. Unfortunately, there is little or no consistent data with which to compare this values, but it agrees with scalability concept of the problem and shows that the simulation is functioning as would be expected.
Note that the shortest path is found faster when blockages are present. This is due to the fact that the blockages constrain the search space for the ant colony, thus decreasing the time necessary to find a shortest path. This pattern is present in all of the remaining graphs and so it will only be noted here.
Explore Rate of the Ant
The second feature of this ant simulation that was investigated was the effect of ant exploration on the ant colonies ability to converge on a shortest path. In this simulation, the explore rate determines the average number of time frames between performing a more random movement. So, when the explore rate is low (less than 10), one would expect the ants to behave very erratically and rarely converge on any path. However, when the explore rate is high (greater than 100), one would expect the ants to behave so deterministically that they only select the first path they find to a food supply which may not be the shortest path. Hence, there seems to be some optimal explore rate in the range of 10 to 100 which allows the faster convergence to the shortest path.
To test this claim, 25 simulations measuring time to path convergence were run and averaged for each of 3 different ant colony sizes for each of 10 different explore rates with and without blockages. The results are plotted on the following graphs:
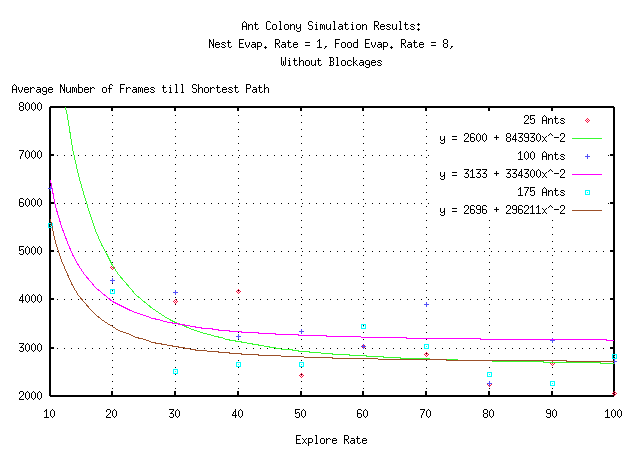
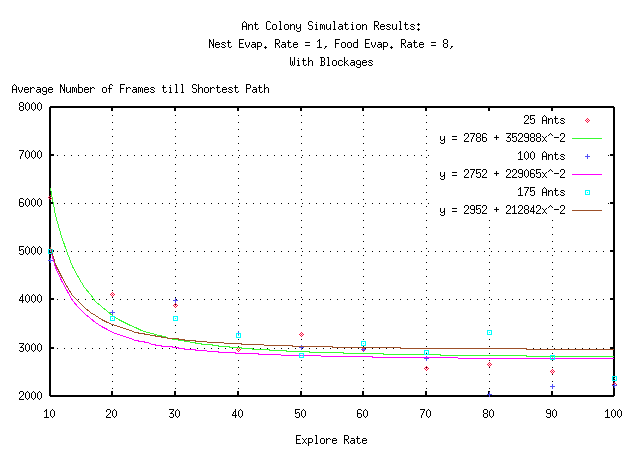
As can be seen from the graphs, there is surprisingly no optimal value of the explore rate. The data appears to be exponentially decaying in all six cases. This implies that the larger the explore rate is, the faster the ant colony converges on a shortest path solution.
Referring back to underlying method at work in the ant colony simulation, an answer can be found for this unobvious result. Recall that the ant simulation does nothing more than generate a stochastically flood-filled gradient map of pheromones around the nest and the food supplies. Thus, when the explore rate is large, an ant deterministically follows the steepest gradient back to the nest. Since, steepest gradient descent always yields the shortest distance between an ant and the nest, the ant always find the shortest path back.
Now, this is only true because the terrain was constant throughout the experimental trials. The randomness present with lower values of the explore rate are necessary to allow for continued exploration of new shortest paths on a dynamic terrain. Otherwise, the ants will never abandon a path once they have converged on it, regardless of the presence of shorter paths.
Optimality of the Ants Colony Paths
The last question remaining is how optimal the paths discovered by the ant colony are compared to the actual shortest path. Because the ant colony is secretly using gradient descent, one would expect the ant colony to converge to a path within a small percentage of optimal. To answer this question, 25 simulations measuring the path length were run and averaged for each of 3 different ant colony sizes for each of 10 different explore rates with and without blockages. The results are plotted on the following graphs:
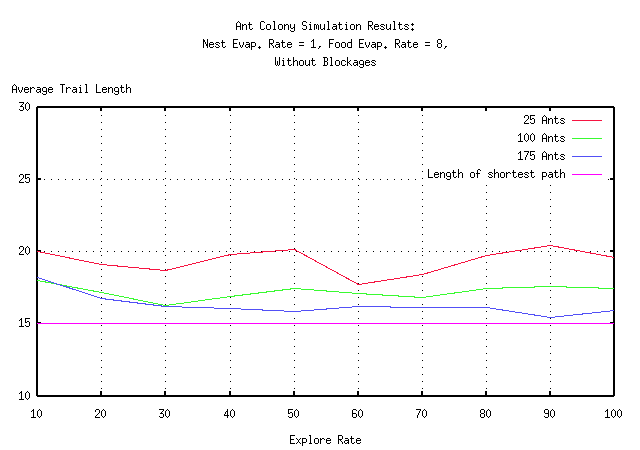
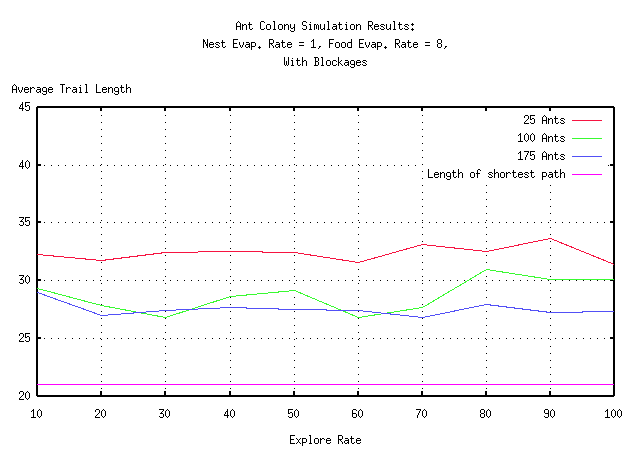
It can seen from the graphs that the explore rate has little if any affect on the average path length. The greater the number of ants, the closer to optimal the path lengths seem to become. Of more importance is the fact that regardless of the number of ants, the explore rate, or blockages, the path discovered by the ant colony is always within 50% of optimal. This is very important since it implies that the ant colonies were not actually discovering the shortest paths in the previous graphs. However, the paths are guaranteed to be within 50% of optimal, so the results for the previous section still hold.
Conclusion
The ant simulator successfully attained the goals set forth in the problem statement. It provides a robust, interactive environment for investigating the various properties of ant colonies and the convergence of ant colonies to shortest paths. The following list summarizes the investigated parameters of the ant simulation:
- Number of Ants: For each ant added to a colony, the ant colony converges to a path within 50% of the optimal shortest path about 3 time frames faster. This proves that the model, just as in real life, is scalable.
- Explore Rate: The most surprising result of the project was that the time it takes to converge to a path within 50% of the optimal shortest path decays exponentially as the explore rate is increased. Furthermore, the explore rate has no affect on the length of the path discovered by the ant colony.
- Optimality of the Paths: The most reassuring result of the project is that the ant colony will always converge to a path within 50% of the optimal shortest path.
By far the most intriguing aspect of this simulation is actually interacting with the ant via adding and removing blockages to their environment. No graphs or words can replace the experience of downloading and investigating the properties of the ant simulator oneself!