Week 2 Goals
Modify the implementation to handle evaporation of the pheromone trails and arbitrary blockages in the environment. This new method will be tested to see if it still finds the shortest path solution. This will introduce new unknown parameters and possibly change the old parameters, so these will be compared to the values from the previous method.
Week 2 Results
This week required many major changes to the code from the previous week. The first change was adding the evaporation of the pheromone trails which is simply implemented by decrementing the amount of pheromone on each grid cell by some specified evaporation constant every time step. The second change was the addition of a new command line parameter to specify a blockage map which contains the location of the static blockages in the environment.
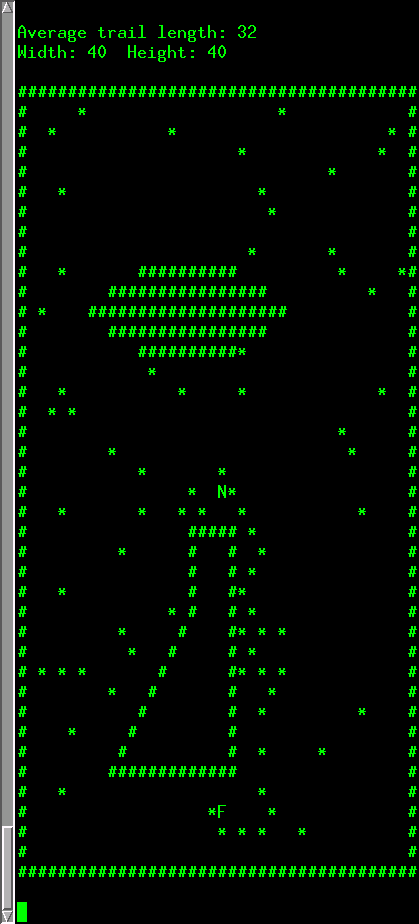
The addition of blockages meant that I could no longer assume a line of sight to the nest for all ants which is the assumption I had made in my previous week's algorithm. My solution was to have the ants lay two distinct pheromone scents. When an ant leaves the nest, it leaves "nest" scent as it searches for food. When an ant leaves a food supply, it leaves a "food" scent as it walks towards the nest. Furthermore, the strength of the pheromone left on a grid cell is inversely proportional to the number of steps the ant has taken away from the nest or the food supply.
This system turns the grid into a pheromone gradient map where the stronger a pheromone scent is, the closer it is to a nest or a food supply. Thus, the ants can traverse the environment by following the gradients. This solves the problem of navigating around blockages (see the screenshot below) and determining the final destination of a trail. There is a good deal of physical evidence that many species of ants use this technique to explore the area surrounding their nests.
Once the pheromone system had been updated, it was necessary to devise new rules for the movement of the ants. In the end, I settled on the following set of rules. First, let U, D, L, and R be the pheromone levels in the up, down, left, and right directions, respectively. Also, let T = U + D + L + R. When an ant is looking for food, it moves either up, down, left, or right with a probability of U/T, D/T, L/T, or R/T, respectively, where the pheromone levels in question are the Nest to Food type. Once an ant has food, it moves in the direction of the greatest pheromone level where the pheromone type is Food to Nest. This will causes the ant to take the shortest path back to the nest from food, but allow the ant to probabilistically explore the environment on the way to food from the nest.